Introduction
Testing a proposed model against simulated data generated from a known underlying process is an important but sometimes overlooked step in ecological research (Lotterhos, Fitzpatrick, and Blackmon 2022; Austin et al. 2006). In fisheries science, simulation testing is commonly used to evaluate stock assessment and population dynamic models and assess their robustness to various types of error (Deroba et al. 2015; Piner et al. 2011). Before applying our size-at-maturity estimation procedures to the actual Jonah crab data, we created multiple simulated data sets with differing characteristics in order to determine the domains of applicability and inference of our model. The domain of applicability refers to the types of situations and data sets to which a model can reliably be applied, while the domain of inference is defined as the processes or conclusions that can be inferred from the model output (Lotterhos, Fitzpatrick, and Blackmon 2022).
Basic simulation steps
- Create normal distribution of crabs with given mean and SD for carapace width (CW)
- Use logistic distribution function with known location and scale parameters (i.e., known L50 and steepness of the logistic curve) to find the probability of maturity for each individual
- Using given parameters for the slope and intercept of the allometric equation, find the predicted chela height (CH) for each individual based on their carapace width
- Add error representing individual variation in allometric growth, which we assume to be log-normally distributed. Variance in empirical size-at-maturity data often appears higher for mature individuals, so by assuming a multiplicative error structure, these errors will be proportional to the x-axis variable. For example, a measurement error of 4 mm would be less likely to occur when measuring a crab with a carapace that is 30 mm in length (a 13% error) than for a crab with a 100-mm carapace (a 4% error).
- Use different combinations of logistic and allometric parameters to determine how the model approach performs given varying possibilities for the true underlying biological process. We will also include several possibilities for the amount of noise present in the data by changing the magnitude of both types errors. The collection of parameter sets will include some extreme combinations that represent challenging or “adversarial” data sets. Such simulations help determine the domain of applicability by assessing model performance across a range of biologically realistic data sets that capture the variation and imperfection found in empirical data (Lotterhos, Fitzpatrick, and Blackmon 2022).
Equations
The parameterization of the logistic equation we will use is: f(x)=\frac{1}{1+e^{-(x-a)/b}} where a is a location parameter and b is the shape parameter.
The allometric growth equation is Y=\beta X^{\alpha}
which results in a linear plot when log-transformed: \log{(Y)}= \tilde{\beta}+\alpha\log{(X)}. Here, \alpha is the slope of the allometric line and \beta is the intercept, with \tilde{\beta}=\log{(\beta)}. Differences in the intercept of the allometry indicate differences in the proportionate size of the chela, irrespective of carapace width. In contrast, differences in the slope parameter represent differences in how the relative size of the chela changes with body size.
A note on the error distribution
We assume that the errors added in Step 4 are normally distributed around the regression lines obtained by log-transforming the raw CW and CH values. In other words, we are assuming the original data has multiplicative log-normally distributed error:
Y=\beta X^{\alpha}e^{\varepsilon}, \quad \varepsilon \sim N(0,\sigma^2) \log{(Y)}=\log{(\beta)}+ \alpha\log{(X)}+\varepsilon, \quad \varepsilon \sim N(0,\sigma^2)
The question of whether error structures should be assumed to be multiplicative or additive when fitting allometric models is non-trivial and often controversial (Packard 2009; Ballantyne 2013; Xiao et al. 2011). However, the assumption of multiplicative error is often appropriate for biological contexts and in this case, simulating error based on a multiplicative structure generates artificial data sets that adequately resemble the empirical morphometric data sets we are interested in (Xiao et al. 2011; Kerkhoff and Enquist 2009). Alternative error distributions for allometric models continue to be developed, and future extensions of our research could consider the performance of various size-at-maturity models when applied to simulated data with different forms of error (Echavarría-Heras et al. 2024).
Default parameters
Let’s visualize some characteristics of the underlying data set (without error) when called with the default parameters. The default is for the function to generate a random sample of 1000 crabs with a mean carapace width of 105 mm and standard deviation of 20 mm. The true size at maturity for the population is 100 mm, and the slope parameter for the logistic equation is 5. There is no change in the allometric slope or intercept parameters (\alpha=1.2, \beta=0.15) upon reaching maturity, so if this was real data, we would not actually be able to estimate size at maturity based on a change in morphometric ratios. The SD of the error distribution also remains constant upon reaching maturity.
default_sim <- fake_crustaceans()
default_sim_long <- default_sim %>%
rename(reg_x = x, reg_y = y) %>%
tidyr::pivot_longer(
cols = c(reg_x, reg_y, log_x, log_y),
names_sep = "_",
names_to = c("log", "var")
) %>%
mutate(log = if_else(log == "log", TRUE, FALSE))
#visualize crab size distribution
ggplot() +
geom_histogram(data = default_sim, aes(x = x), bins = 35) +
labs(x = "Carapace width (mm)", y = "Count") + mytheme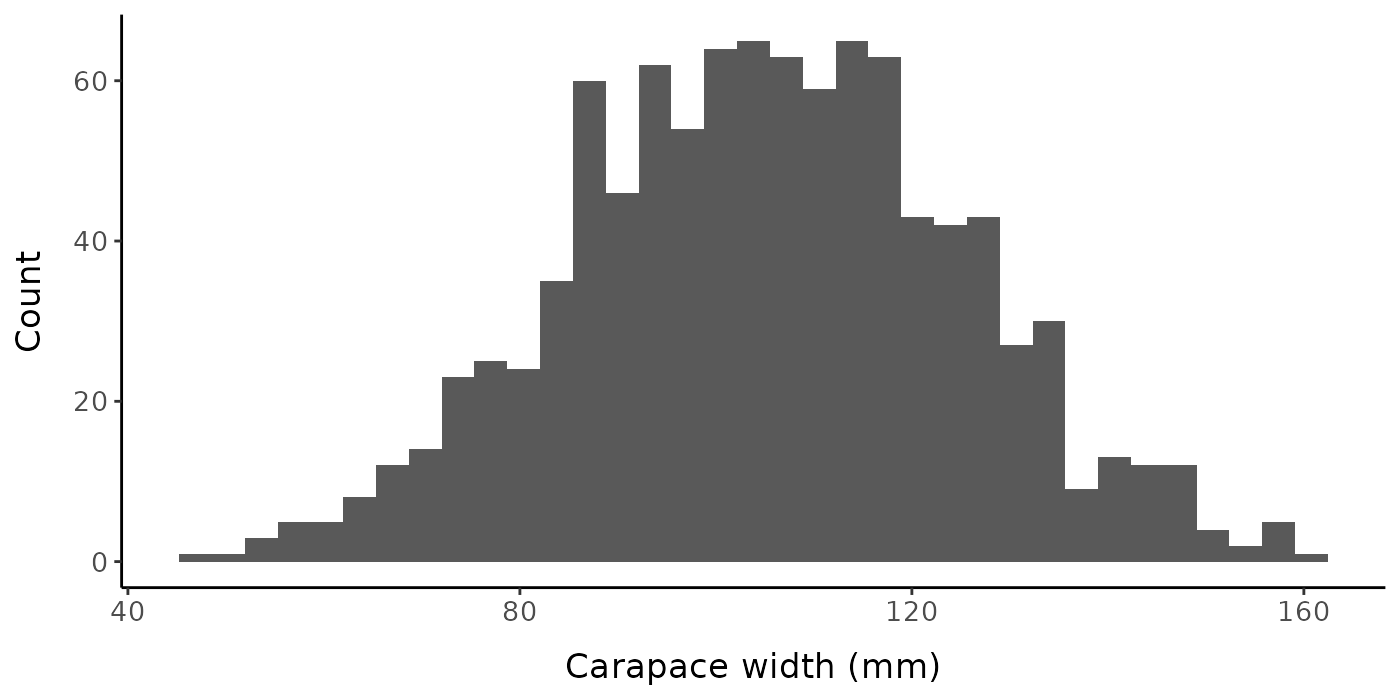
Histogram of carapace widths
#Size by maturity stage histogram
ggplot() +
geom_density(data = default_sim,
aes(x = x, group = mature, color = mature, fill = mature), alpha = 0.5) +
mytheme +
labs(fill = NULL, color = NULL, x = "Carapace width (mm)", y = "Density") +
scale_color_manual(values = c("0" = "#368aab", "1" = "#993843"),
breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
scale_fill_manual(values = c("0" = "#7bbcd5", "1" = "#CA6E78"),
breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature"))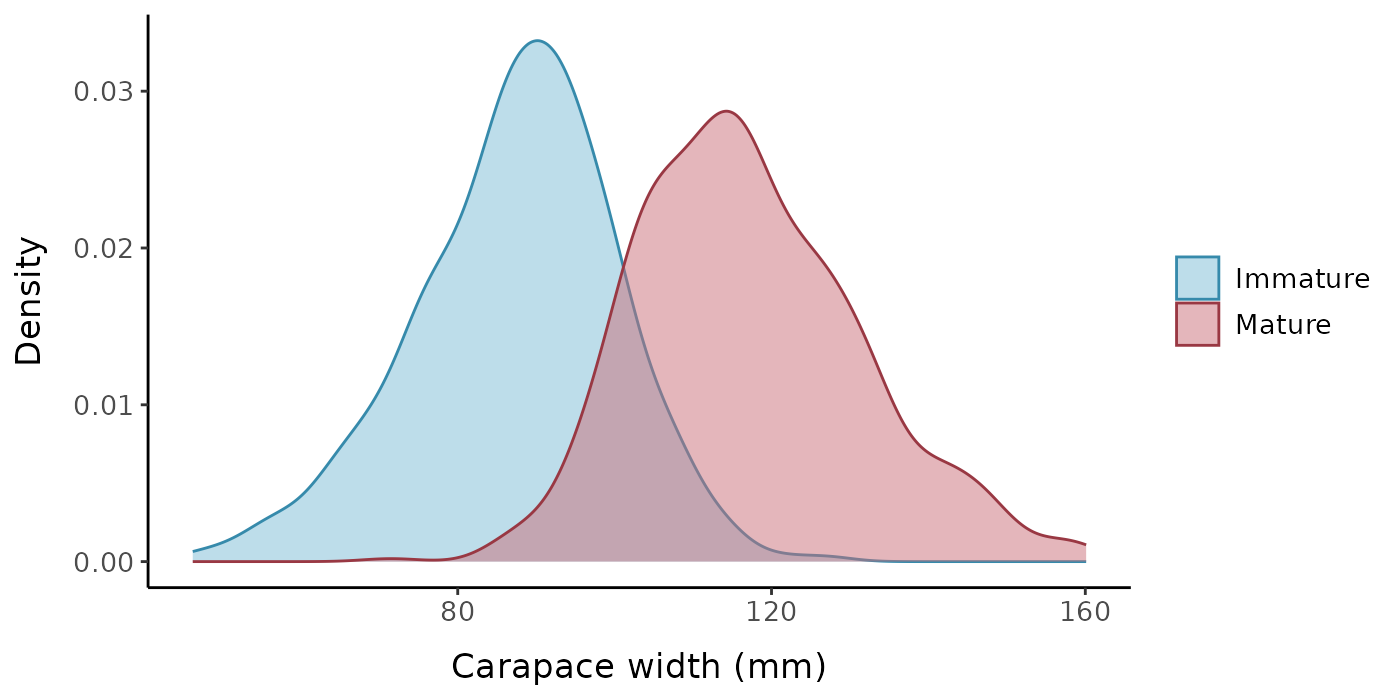
Distribution of carapace widths by maturity level
Now we finally plot our two variables of interest:
temp_df <- default_sim_long %>% pivot_wider(names_from = var)
ggplot(data = temp_df, aes(x = x, y = y, color = mature)) +
geom_point(alpha = 0.5, size = 1) +
facet_wrap(~log, scales = "free",
labeller = as_labeller(
c("FALSE" = "Normal scale", "TRUE" = "Log scale"))) +
mytheme +
labs(x = "Carapace width (mm)", y = "Chela height (mm)", color = NULL) +
scale_color_manual(values = c("0" = "#7bbcd5", "1" = "#CA6E78"),
breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
geom_vline(data = filter(temp_df, log == TRUE), aes(xintercept = log(100)),
lty = "dashed", color = "grey") +
geom_vline(data = filter(temp_df, log == FALSE), aes(xintercept = 100),
lty = "dashed", color = "grey")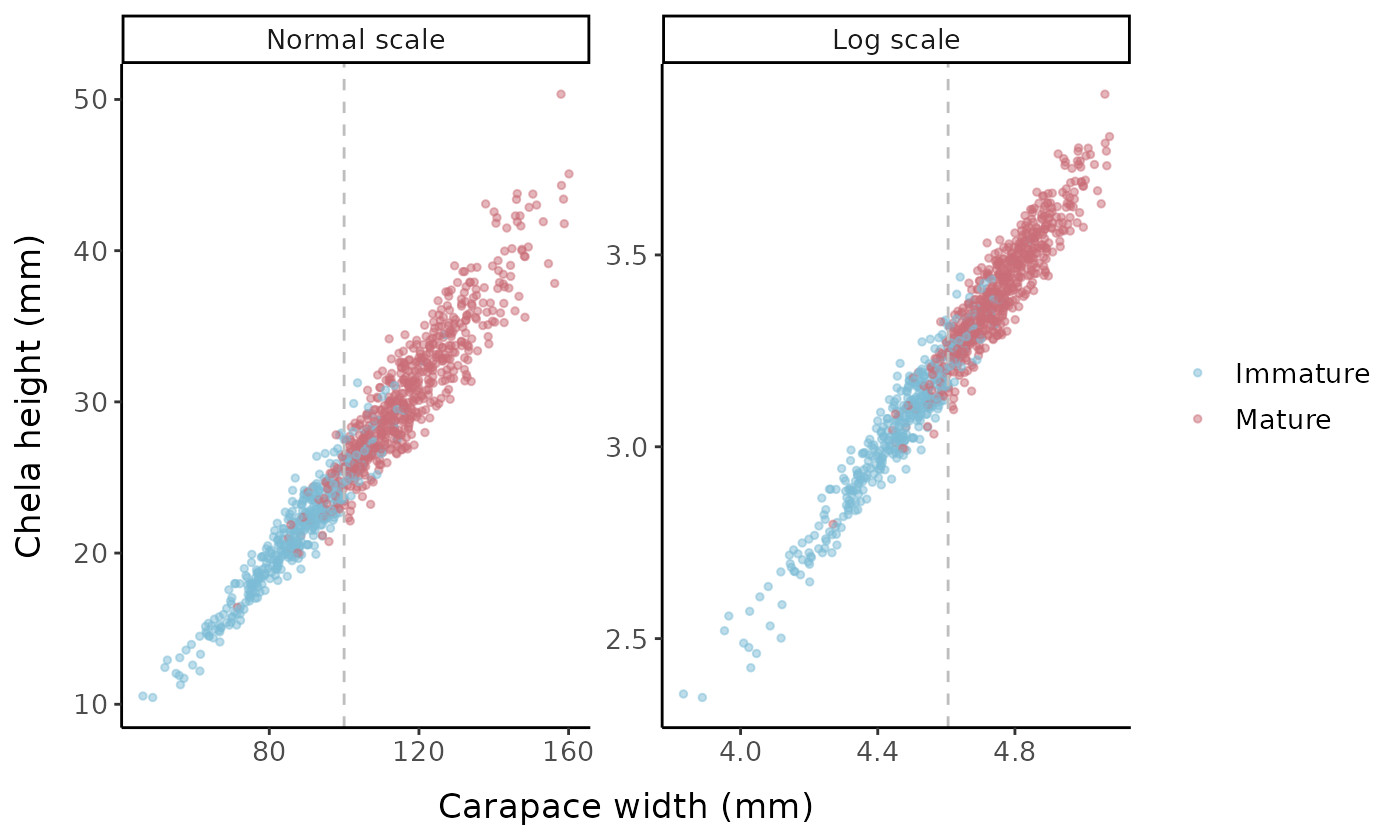
Carapace width vs. chela height using the default simulation parameters. Vertical grey lines represent the size at maturity used in the logistic equation (100 mm).
Changing parameters
Setup
Now, we will adjust the input values to our simulation function to generate more realistic data. We will change the parameters in three ways: the slope of the logistic curve (the sharpness of the transition to maturity), the allometric slope and intercept, and the magnitude of the error in the data.
Instead of leaving the slope parameter at 5, we will try values from 1 to 10. Values above 10 were initially tested, but the degree of overlap between the mature and immature groups was far beyond what is likely to be observed in nature.
slope_options <- c(1:10)We will test five different options for how allometric growth changes upon reaching maturity, including the default of no change.
# Create data frame of allometric parameter vectors
params_df <- tribble(
~ name, ~ vec,
# No change in the slope or intercept - default
"no_change", c(1.2, 0.1, 1.2, 0.1),
# No change in the slope, slight increase in the intercept: the relative size
# of chela is the same with varying CWs within a maturity stage, but becomes
# proportionally larger upon reaching maturity.
"parallel", c(1.1, 0.1, 1.1, 0.15),
# Slight increase in the slope, no change in the intercept. The relative size
# of the chela does not become proportionately larger upon reaching maturity,
# but the rate at which chela size increases with increasing body size is
# higher for adult crabs compared to juveniles (goes from allometric to
# slightly hyperallometric).
"allo_to_hyper", c(1, 0.2, 1.1, 0.2),
# Moderate increase in the slope, moderate decrease in the intercept. The
# relative size of the chela becomes smaller upon reaching maturity, but the
# rate at which chela size increases with increasing body size is higher for
# adult crabs compared to juveniles (goes from allometric to hyperallometric).
"crossing", c(1, 0.25, 1.25, 0.08),
# Large increase in the slope, large decrease in the intercept. The relative
# size of the chela becomes much smaller upon reaching maturity, but the rate
# at which chela size increases with increasing body size is much higher for
# adult crabs compared to juveniles (goes from slightly hypoallometric to
# hyperallometric).
"hypo_to_hyper", c(0.9, 0.27, 1.75, 0.006)
) We will test three options for the magnitude of the errors. The three options will be a normal distribution with an extremely small SD (essentially no error), a SD equal to 1/20 the range of the x-axis variable, or a SD of 1/15 the range of the x-axis variable.
err_options_df <- tribble(
~errs, ~err,
"none", 10^9,
"low", 20,
"high", 15)Now create data frame with all possible combinations of these parameters and create a simulated data set for each combination.
params_df <- expand_grid(params_df, slope_options)
err_params_df <- params_df %>% expand_grid(err_options_df)
fake_crustaceans <- err_params_df %>%
rowwise() %>%
mutate(output = list(
fake_crustaceans(
allo_params = vec,
slope = slope_options,
error_scale = err
)
)) %>%
unnest(output)Visualization
We can see how the slope of the logistic distribution becomes less steep with higher values of a. The lower values are representative of a species where there is very little intraspecific variation in size at maturity; if the true L50 is 100 mm, almost all individuals will become mature close to 100 mm. In contrast, the high parameters represent a species where there is significant variation in L50 between individuals.
pal <- c("#5D74A5", "#819AC2", "#A6C1DF", "#CAD9DC", "#ECEDCE",
"#F9E3B6", "#F1BD96", "#E39778", "#C57663", "#A8554E")
# Logistic curves with different slope parameters
ggplot()+
geom_line(data = fake_crustaceans,
aes(x = x, y = prob_mat, color = as.factor(slope_options)),
linewidth = 1)+
theme_light()+
geom_vline(xintercept = 100, lty = "dashed",
color = "gray2", linewidth = 0.5)+
scale_color_manual(values = pal)+
labs(x = "Carapace width (mm)", y = "Probability of maturity",
color = "Slope parameter")+
theme(
axis.title.y = element_text(margin = margin(t = 0, r = 10, b = 0, l = 0)),
axis.title.x = element_text(margin = margin(t = 10, r = 0, b = 0, l = 0)),
text = element_text(size = 13))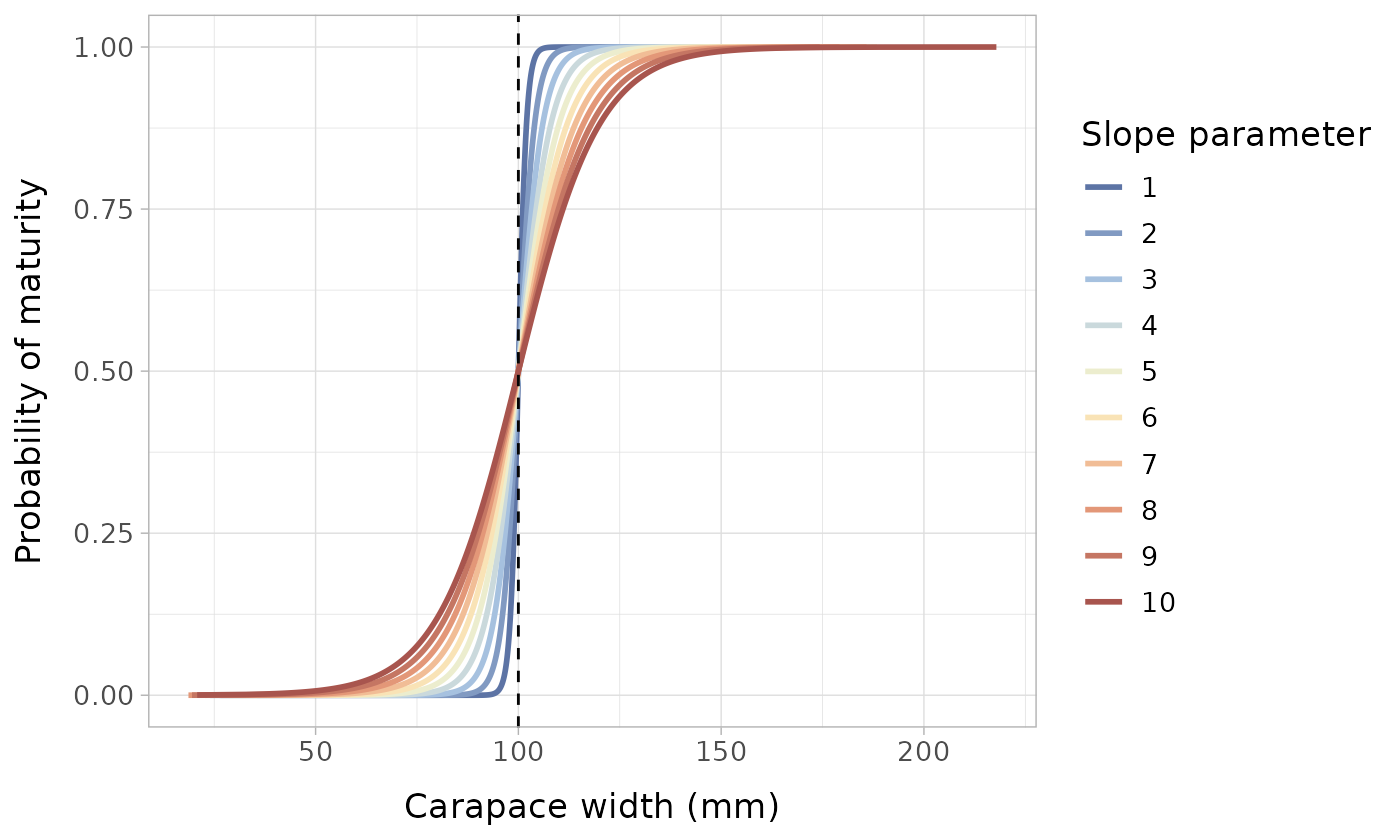
Probability of maturity function with varying slope parameters. The vertical dashed line represents the size at maturity/inflection point/location parameter, which is set to 100 mm.
Another way of visualizing the impact of changing the slope parameter (a) is by comparing density plots of maturity by CW. We can see that the area of intersection between the immature and mature curves increases with increasing values of a. The right tail of the immature distribution extends to much higher CW values when a=10 compared to when a=1, while the left tail of the mature distribution extends much lower.
#Size by maturity stage density plots
fake_crustaceans %>%
filter(slope_options %in% c(1, 4, 7, 10)) %>%
ggplot() +
geom_density(aes(x = x, group = mature, color = mature, fill = mature),
alpha = 0.5) +
mytheme +
facet_wrap(~slope_options, ncol = 1) +
labs(fill = NULL, color = NULL, x = "Carapace width (mm)", y = "Density") +
scale_color_manual(
values = c("0" = "#368aab", "1" = "#993843"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
scale_fill_manual(
values = c("0" = "#7bbcd5", "1" = "#CA6E78"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature"))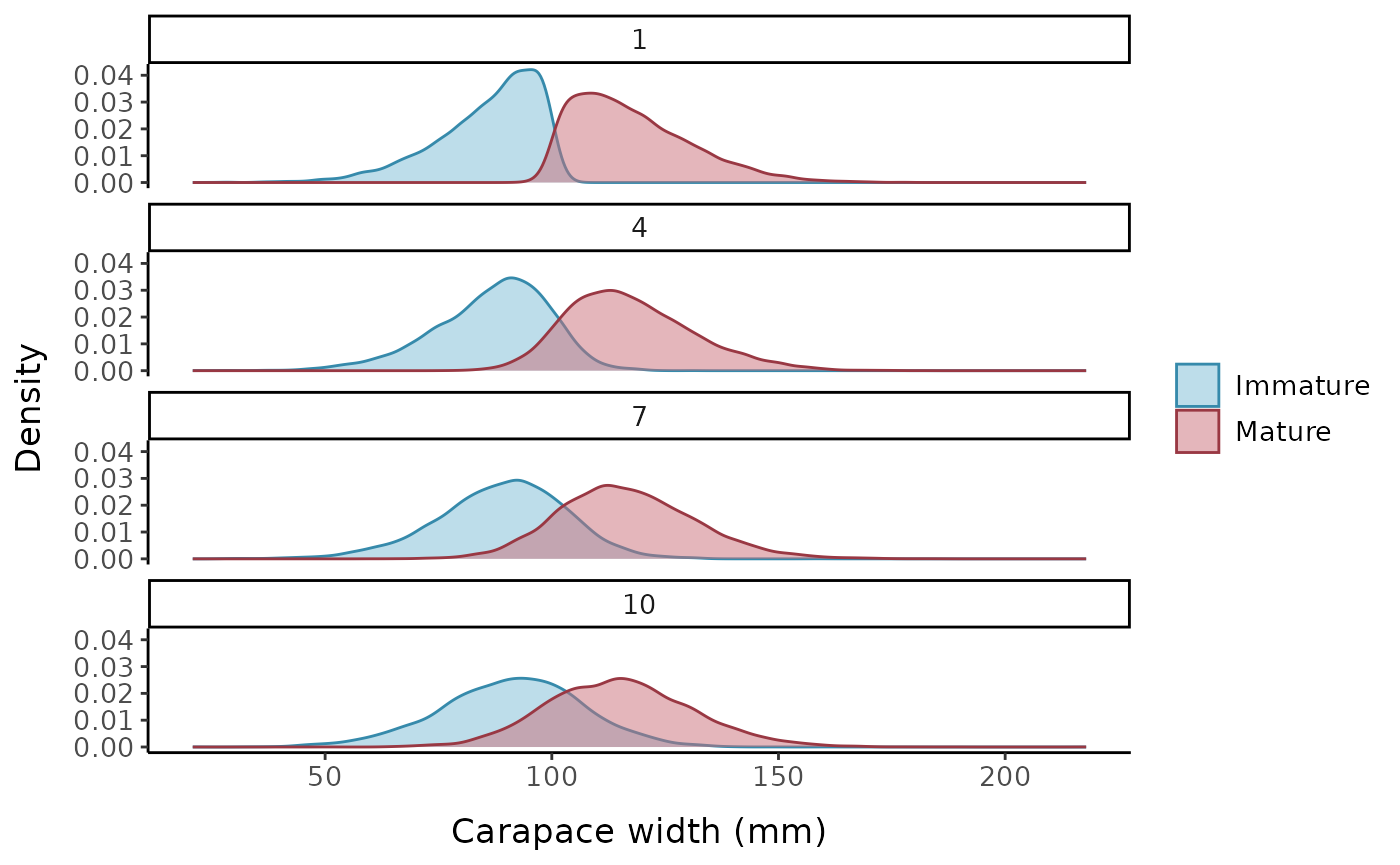
Density plots illustrating smoothed distributions of mature and immature crabs over a range of carapace widths for four different values controlling the shape of the underlying logistic function.
Let’s visualize the data with the default slope parameter of 5 and minimal error:
# Lines only - original scale
fake_crustaceans %>% filter(slope_options == 5, errs == "none") %>%
ggplot() +
geom_point(aes(x = x, y = y, color = mature), size = 1, alpha = 0.5) +
facet_wrap(~name) +
mytheme +
labs(x = "Carapace width (mm)", y = "Chela height (mm)", color = NULL) +
geom_vline(xintercept = 100, lty = "dashed", color = "gray") +
scale_color_manual(values = c("0" = "#7bbcd5", "1" = "#CA6E78"),
breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature"))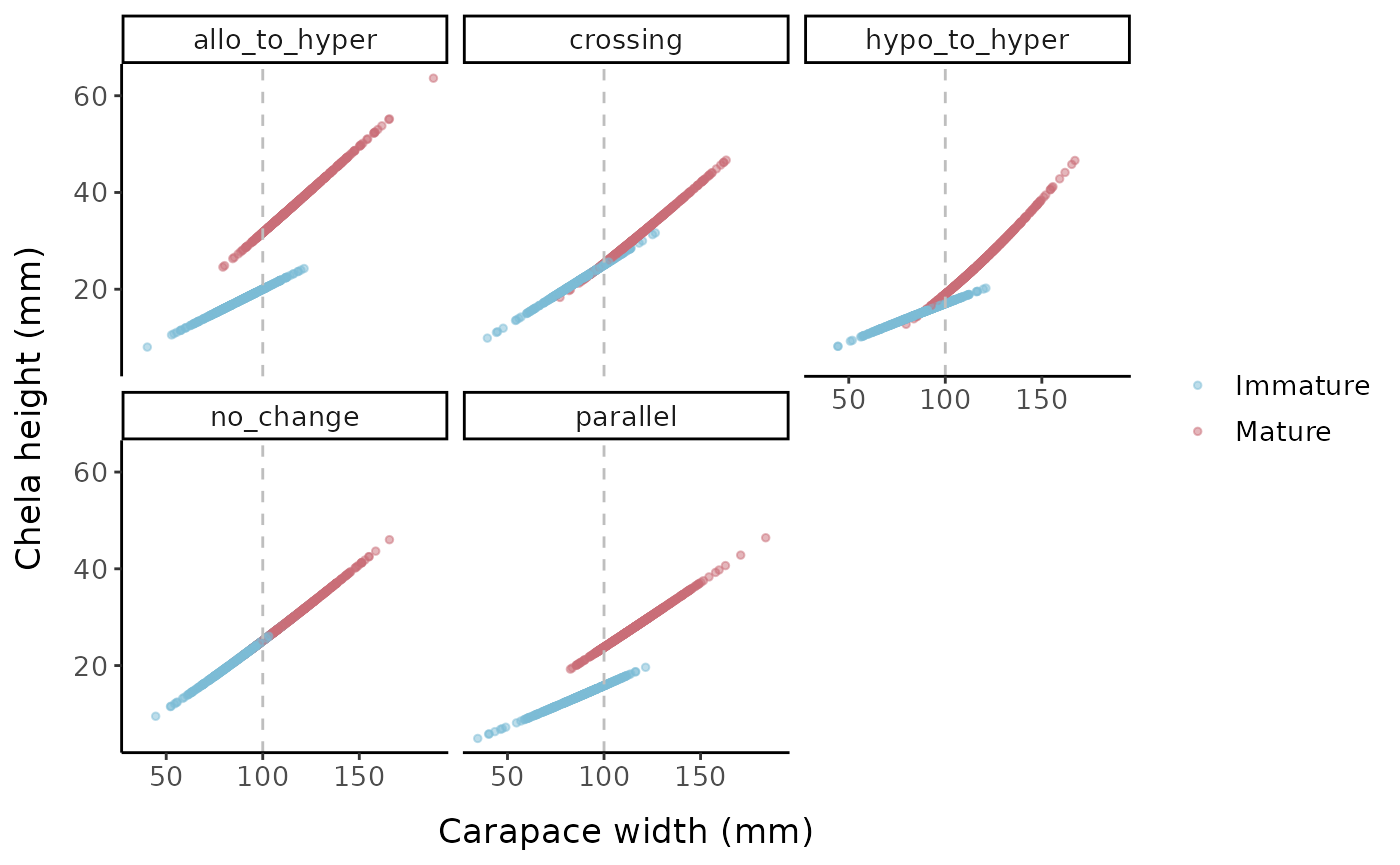
Chela height (mm) vs. carapace width (mm) for the different allometric parameter sets
# Lines only - log scale
fake_crustaceans %>%
filter(slope_options == 5, errs == "none") %>%
ggplot() +
geom_point(aes(x = log_x, y = log_y, color = mature), size = 1, alpha = 0.5) +
facet_wrap(~name) +
mytheme +
labs(x = "Log carapace width (mm)",
y = "Log chela height (mm)",
color = NULL) +
geom_vline(xintercept = log(100), lty = "dashed", color = "gray") +
scale_color_manual(values = c("0" = "#7bbcd5", "1" = "#CA6E78"),
breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature"))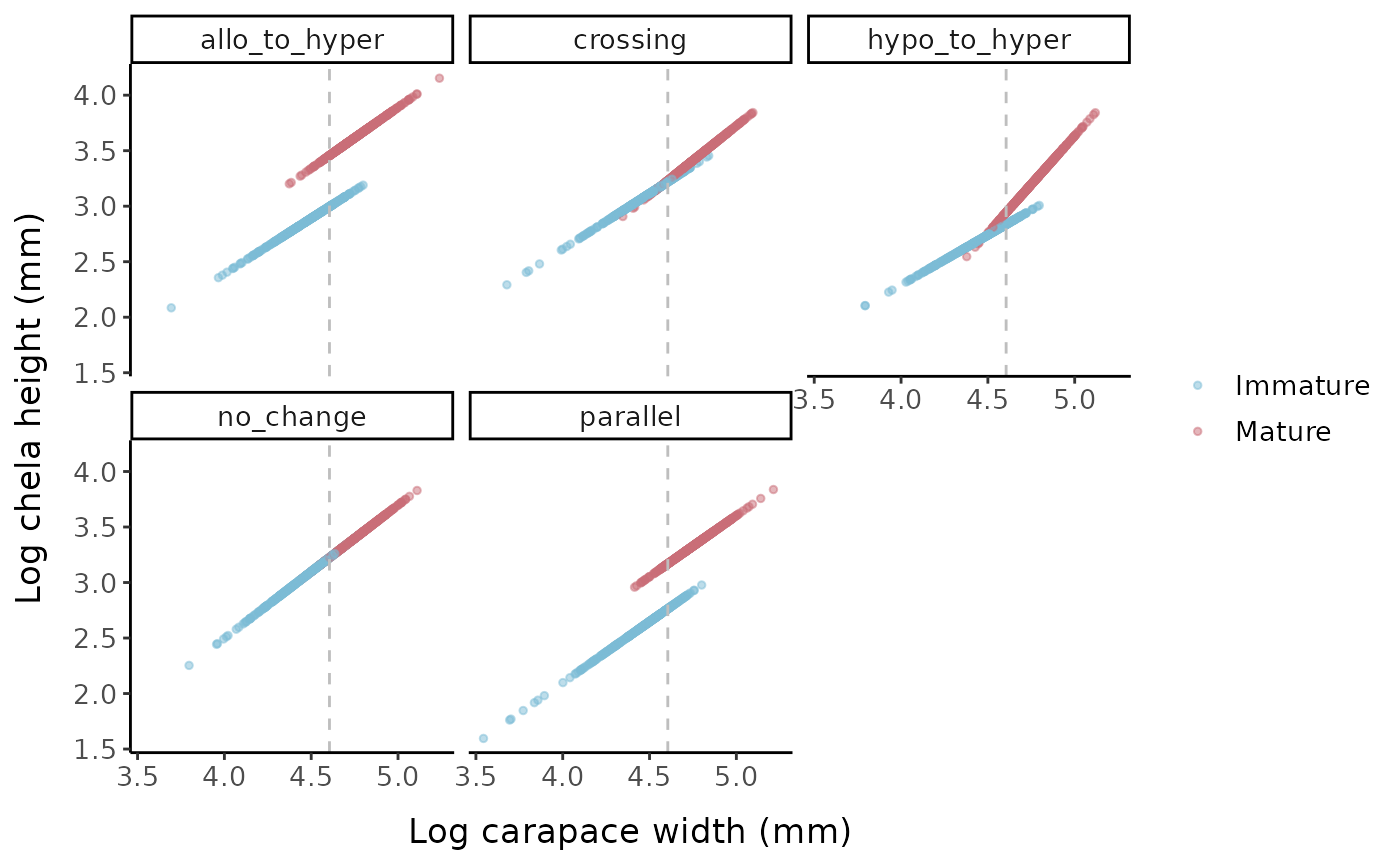
Log chela height vs. log carapace width for the different allometric parameter sets
Now we add data points for the three different error levels:
# Points and lines for one shape parameter and 3 error combos - original scale
fake_crustaceans %>% filter(slope_options == 5) %>%
ggplot() +
geom_vline(xintercept = 100, lty = "dashed", color = "gray") +
geom_point(aes(x = x, y = y, color = mature, fill = mature),
alpha = 0.5, shape = 21, size = 1, stroke = 0) +
facet_grid(errs ~ name) +
mytheme +
labs(x = "Carapace width (mm)", y = "Chela height (mm)",
color = NULL, fill = NULL) +
scale_color_manual(
values = c("0" = "#368aab", "1" = "#993843"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
scale_fill_manual(
values = c("0" = "#7bbcd5", "1" = "#CA6E78"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
guides(lty = "none",
color = guide_legend(override.aes = list(size = 3, alpha = 1))) +
scale_x_continuous(breaks = c(100, 200))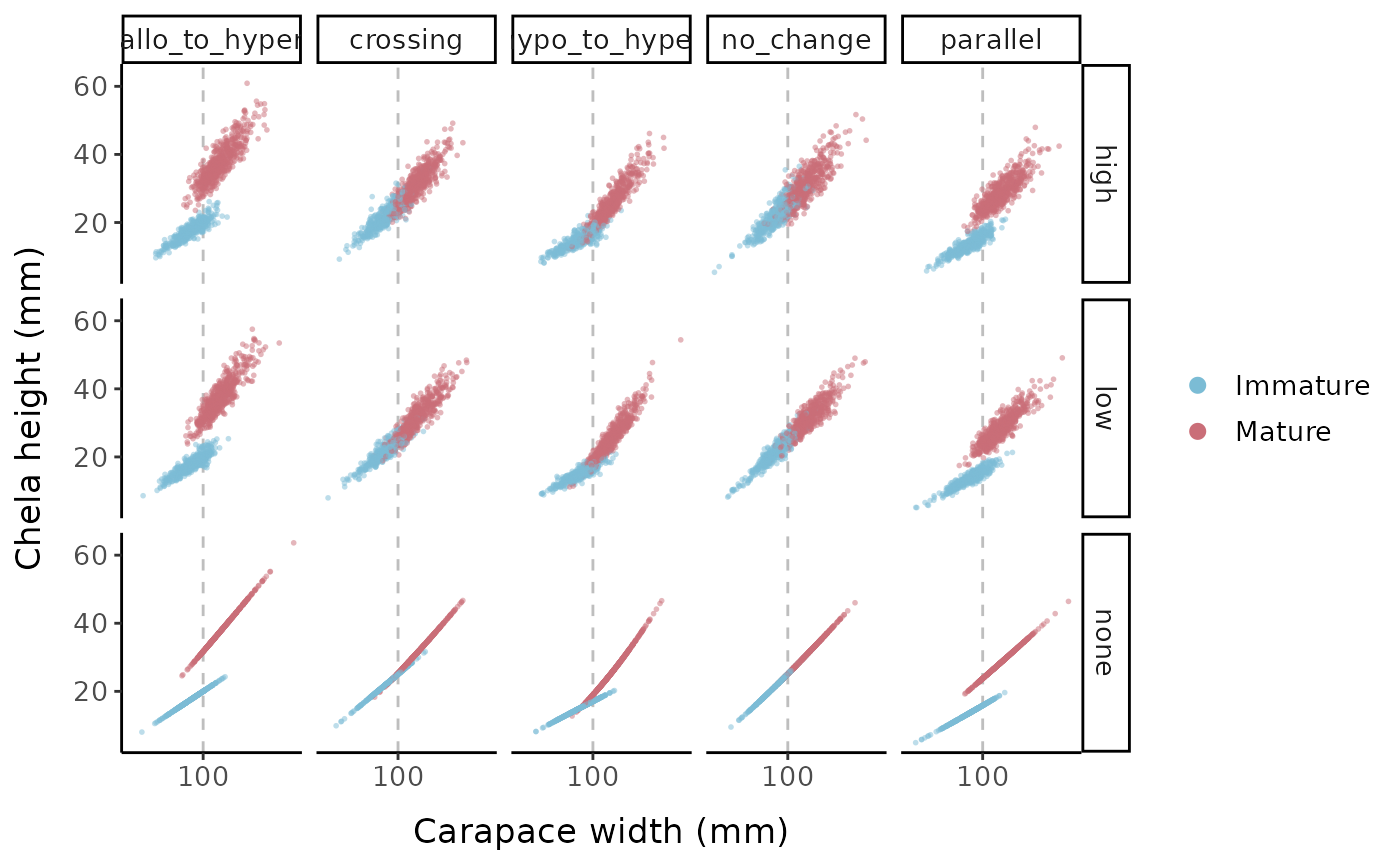
Chela height (mm) vs. carapace width (mm) for the different allometric parameter sets and error options
# Points and lines for one shape parameter and 3 error combos - log scale
fake_crustaceans %>% filter(slope_options == 5) %>%
ggplot() +
geom_vline(xintercept = log(100), lty = "dashed", color = "gray") +
geom_point(aes(x = log_x, y = log_y, color = mature, fill = mature),
alpha = 0.5, shape = 21, size = 1, stroke = 0) +
facet_grid(errs ~ name) +
mytheme +
labs(x = "Log carapace width (mm)", y = "Log chela height (mm)",
color = NULL, fill = NULL) +
scale_color_manual(
values = c("0" = "#368aab", "1" = "#993843"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
scale_fill_manual(
values = c("0" = "#7bbcd5", "1" = "#CA6E78"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
guides(lty = "none",
color = guide_legend(override.aes = list(size = 3, alpha = 1))) +
scale_x_continuous(breaks = c(3, 4, 5))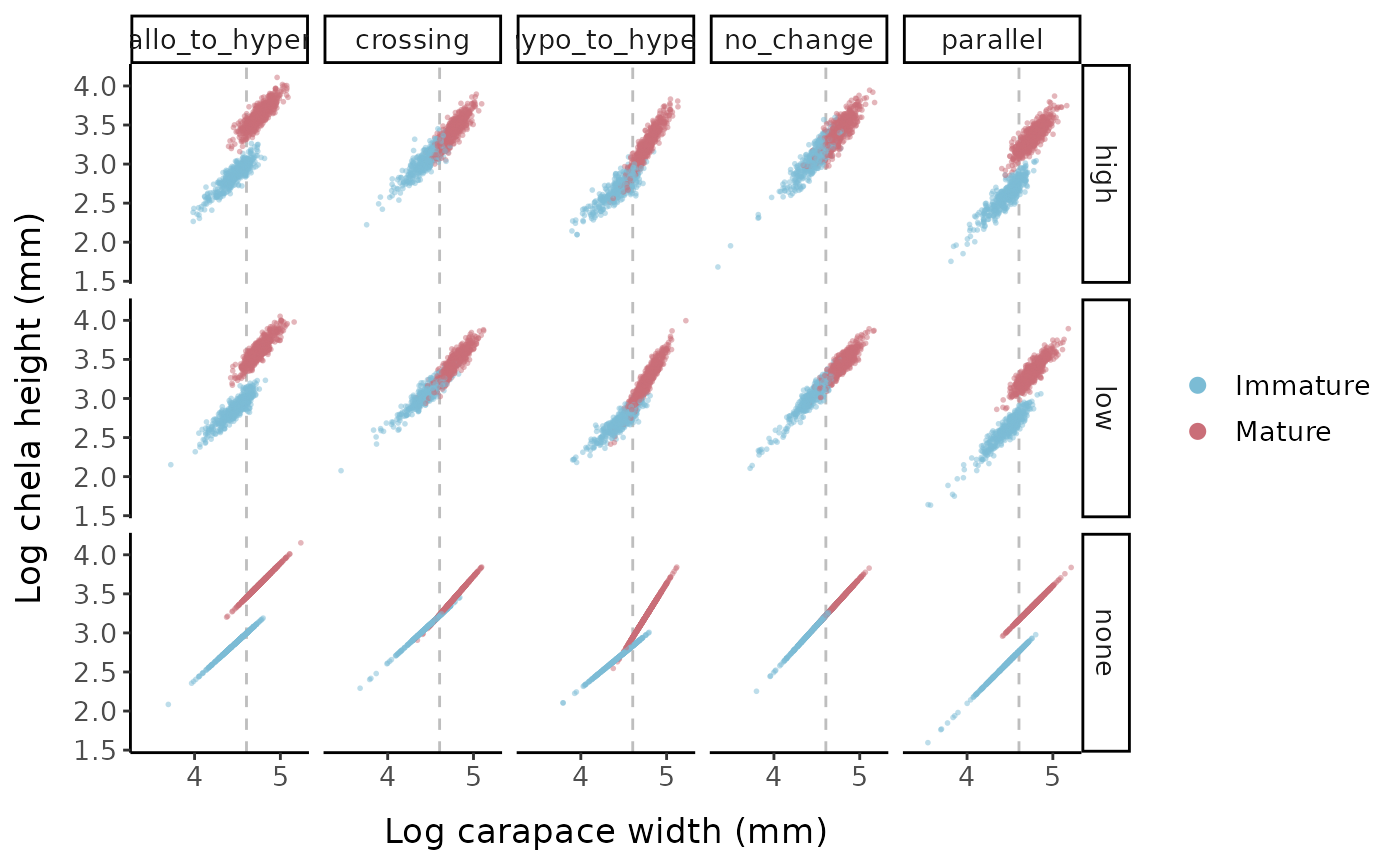
Log chela height vs. log carapace width for the different allometric parameter sets and error options
Keeping the error levels low, here is what each allometric parameter set looks like when we change the logistic slope parameter:
fake_crustaceans %>%
filter(errs == "low", slope_options %in% c(1, 4, 7, 10)) %>%
ggplot() +
geom_vline(xintercept = 100, lty = "dashed", color = "gray") +
geom_point(aes(x = x, y = y, color = mature, fill = mature),
shape = 21, alpha = 0.5, size = 1, stroke = 0) +
facet_grid(slope_options ~ name) +
mytheme +
labs(x = "Carapace width (mm)", y = "Chela height (mm)",
color = NULL, fill = NULL) +
scale_color_manual(
values = c("0" = "#368aab", "1" = "#993843"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
scale_fill_manual(
values = c("0" = "#7bbcd5", "1" = "#CA6E78"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
guides(lty = "none",
fill = guide_legend(override.aes = list(size = 3, alpha = 1))) +
scale_x_continuous(breaks = c(100, 200))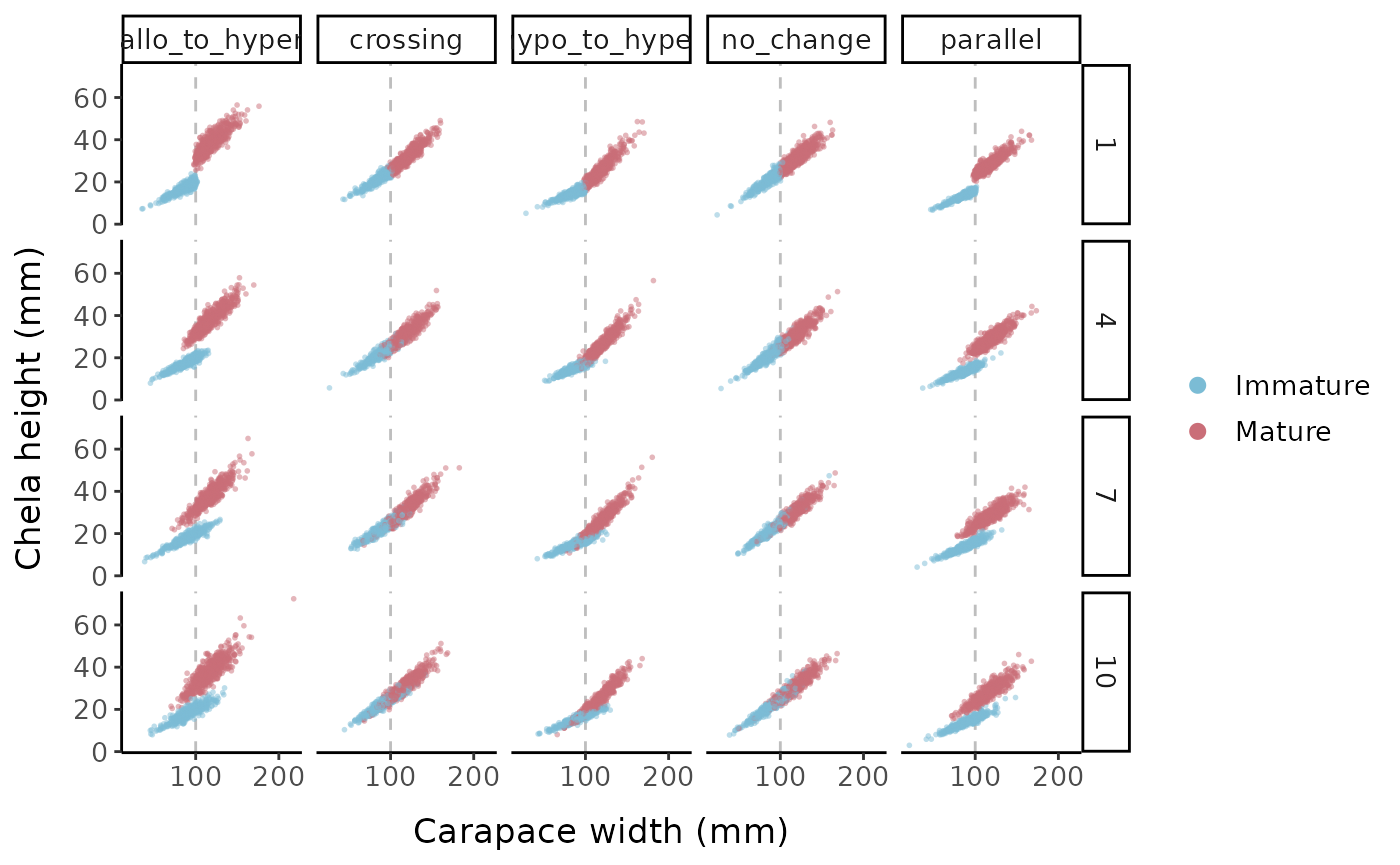
Chela height vs. carapace width for the different allometric parameter sets and logistic slope options
fake_crustaceans %>%
filter(errs == "low", slope_options %in% c(1, 4, 7, 10)) %>%
ggplot() +
geom_vline(xintercept = log(100), lty = "dashed", color = "gray") +
geom_point(aes(x = log_x, y = log_y, color = mature, fill = mature),
shape = 21, alpha = 0.5, size = 1, stroke = 0) +
facet_grid(slope_options ~ name) +
mytheme +
labs(x = "Log carapace width (mm)", y = "Log chela height (mm)",
color = NULL, fill = NULL) +
scale_color_manual(
values = c("0" = "#368aab", "1" = "#993843"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
scale_fill_manual(
values = c("0" = "#7bbcd5", "1" = "#CA6E78"), breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
guides(lty = "none",
fill = guide_legend(override.aes = list(size = 3, alpha = 1))) +
scale_x_continuous(breaks = c(3, 4, 5))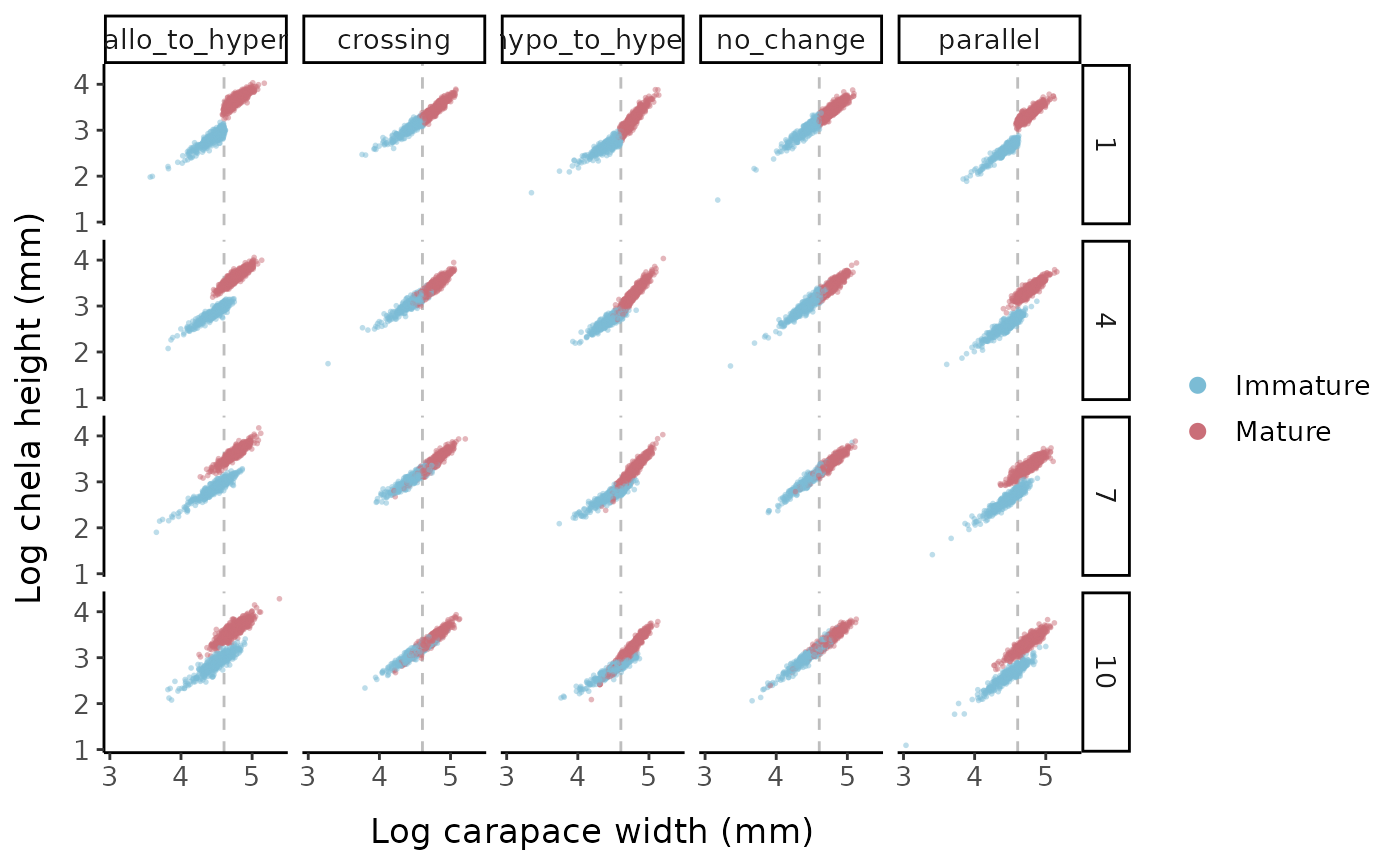
Log chela height vs. log carapace width for the different allometric parameter sets and logistic slope options
