morphmat

We will start by simulating a data set with a known SM50 value of 75 mm to demonstrate an example workflow using morphmat. See vignette("simulations") and the fake_crustaceans() documentation for more details on the structure of our artificial data set.

set.seed(12) # set seed for reproducibility

fc <- fake_crustaceans(
  error_scale = 17,
  slope = 9,
  L50 = 75, # known size at maturity is 75 mm
  n = 800, # sample size
  allo_params = c(0.9, 0.25, 1.05, 0.2),
  x_mean = 85 # mean carapace width of the sample
)

mytheme <- theme_classic() + # define custom theme for ggplots
  theme(
    axis.title.y = element_text(margin = margin(t = 0, r = 10, b = 0, l = 0)),
    axis.title.x = element_text(margin = margin(t = 10, r = 0, b = 0, l = 0)),
    text = element_text(size = 13))

Plot your data

Original scale

ggplot() +
  geom_point(data = fc, aes(x, y), alpha = 0.4) +
  labs(x = "Carapace width (mm)", y = "Claw height (mm)", ) +
  mytheme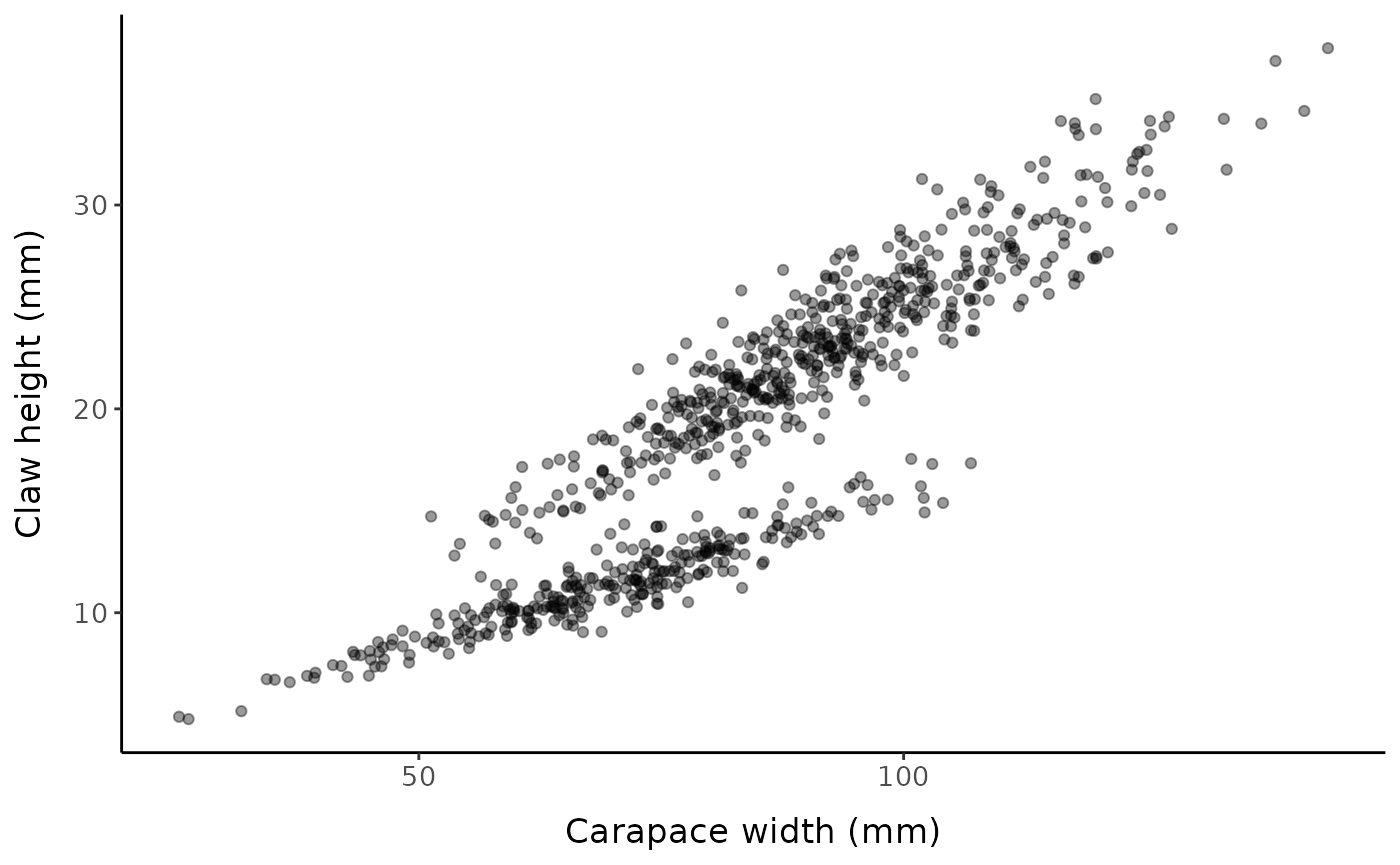

Log-log scale

ggplot() +
  geom_point(data = fc, aes(log_x, log_y), alpha = 0.4) +
  labs(x = "Log carapace width (mm)", y = "Log claw height (mm)", ) +
  mytheme

Suggested method

mclust for classification

clust_dat <- cbind(fc$x, fc$y)
mclust_class <- mclust::Mclust(data = clust_dat,
                               G = 2,
                               modelNames = "EVV")

broom::glance(mclust_class) %>% select(-hypvol)

#> # A tibble: 1 × 6
#>   model     G     BIC logLik    df  nobs
#>   <chr> <int>   <dbl>  <dbl> <dbl> <int>
#> 1 EVV       2 -10582. -5258.    10   800

fc_mclust <- fc %>%
  rename(true_maturity = mature) %>%
  mutate(pred_maturity = mclust_class$classification) 

mature_label <- slice_max(fc_mclust, x) %>% pull(pred_maturity)

fc_mclust <- fc_mclust %>%
  mutate(
    pred_maturity = if_else(pred_maturity == mature_label,
                            as.factor(1), as.factor(0)),
    pred_maturity_num = if_else(pred_maturity == 1,
                                as.numeric(1), as.numeric(0))
  ) %>%
  mutate(uncertainty = mclust_class$uncertainty)

Visualize the mature and immature groups

ggplot(data = fc_mclust) +
  mytheme +
  geom_point(aes(x, y, color = pred_maturity, fill = pred_maturity),
             alpha = 0.5, shape = 21) +
  scale_color_manual(values = c("0" = "#368aab", "1" = "#993843"),
                     breaks = c(0, 1), labels = c("0" = "Immature", "1" = "Mature")) +
  scale_fill_manual(values = c("0" = "#7bbcd5", "1" = "#CA6E78"),
                    breaks = c(0, 1), labels = c("0" = "Immature", "1" = "Mature")) +
  labs(x = "Carapace width (mm)", y = "Chela height (mm)",
       color = "Predicted clusters", fill = "Predicted clusters")

Predicted clusters using mixture-based clustering.

GLM for obtaining SM50 value

This is the most basic way to obtain an SM50 estimate from allometric data that has been clustered into mature and immature groups:

mod <- glm(data = fc_mclust,
           pred_maturity_num ~ x,
           family = binomial(link = "logit"))

unname(-coef(mod)[1] / coef(mod)[2]) # SM50 = -A/B

#> [1] 74.89024

Comparing clustering approaches

all_clusters <- cluster_mods(fc, xvar = "x", yvar = "y", method = c("all"), plot = TRUE)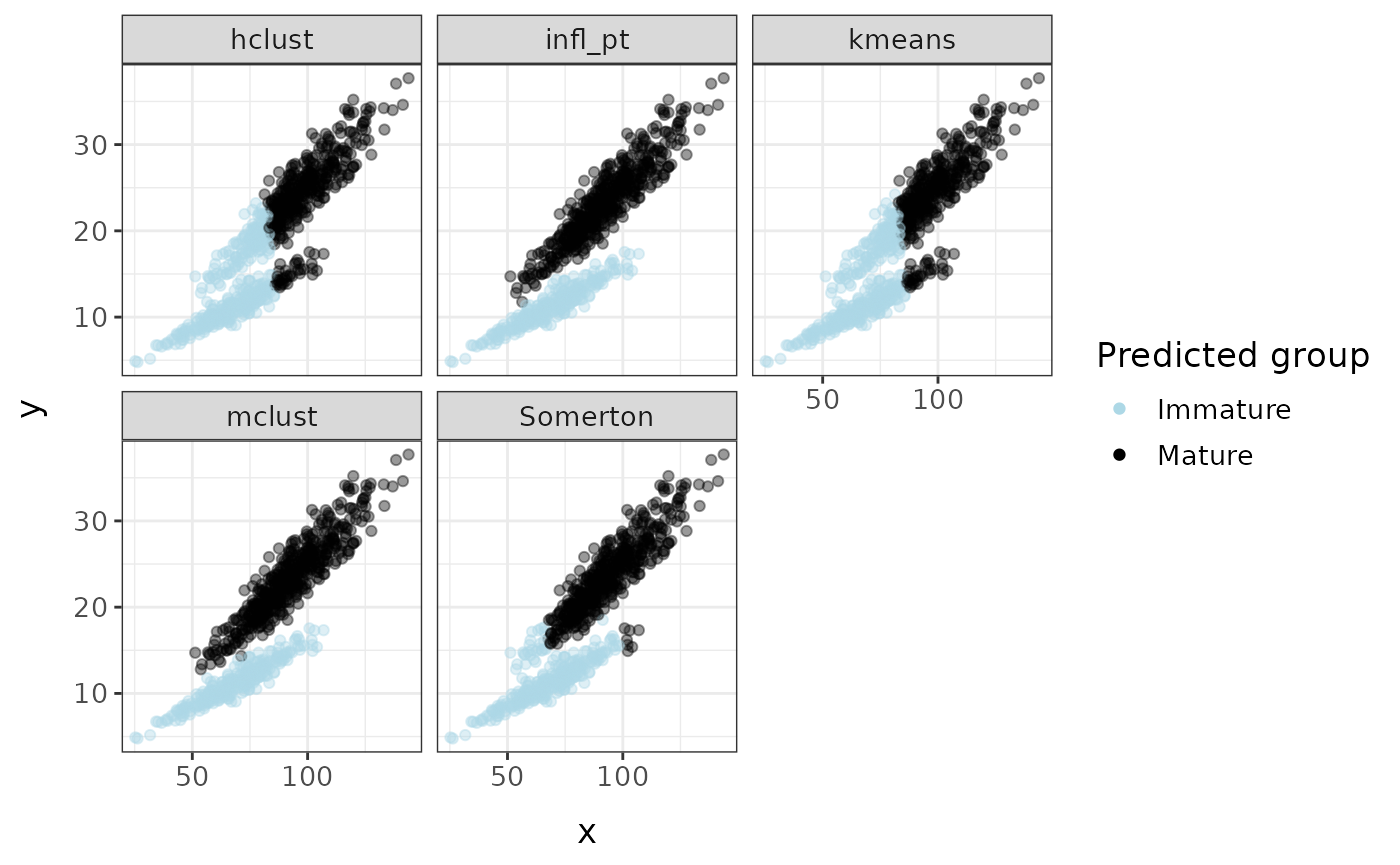

Comparison with piecewise regression models

piecewise_mods(fc, xvar = "x", yvar = "y", method = c("all"))

#>                chngpt             segmented               REGRANS 
#>              67.68312              63.95451              67.67091 
#>               Stevens   Two_line.breakpoint Two_line.intersection 
#>              68.33387              75.43651              56.76587

piecewise_mods(fc, xvar = "x", yvar = "y", method = c("all"),
                   log = TRUE) %>% exp()

#>                chngpt             segmented               REGRANS 
#>              67.68312              62.82577              67.67091 
#>               Stevens   Two_line.breakpoint Two_line.intersection 
#>              68.33387              75.21507              50.25602

Broken-stick/piecewise regression methods - individual functions

REGRANS:

regrans(fc, "x", "y", verbose = FALSE)

#> [1] 67.67091

Two-line logistic:

two_line_logistic(fc, xvar = "x", yvar = "y", verbose = FALSE, SM50_start = 85)

#>    SM50 
#> 77.6817

Two-line model (lines are fit separately; no forced intersection):

two_line(fc, xvar = "x", yvar = "y", verbose = FALSE)

#>   breakpoint intersection 
#>     75.43651     56.76587

Broken-stick Stevens (only iterates over values of the x-axis variable present in the data):

broken_stick_stevens(fc, xvar = "x", yvar = "y", verbose = FALSE)

#> [1] 68.33387