Sources (more will be added): Somerton (1980; D. A. Somerton 1980); Muggeo (2003, 2017; V. Muggeo 2008); Hall et al. (2006)
\begin{equation*}\log{y}= \begin{cases} \tilde{\beta_1} + \alpha_1 \log{x} & \text{for }\log{x} \leq c \\ \tilde{\beta_1} + c(\alpha_1-\alpha_2)+\alpha_2 \log{x} & \text{for }\log{x} > c \end{cases} \end{equation*}
At \log{x}=c, the bottom equation becomes \tilde{\beta_1}+(\log{x})(\alpha_1-\alpha_2)+\alpha_2\log{x}, equivalent to the top equation. Note that in this formulation, there is only one intercept term (\beta_1), so the immature and mature lines cannot have the same slope without being equivalent lines. In this model, the estimated value of the breakpoint parameter c is taken to be SM50.
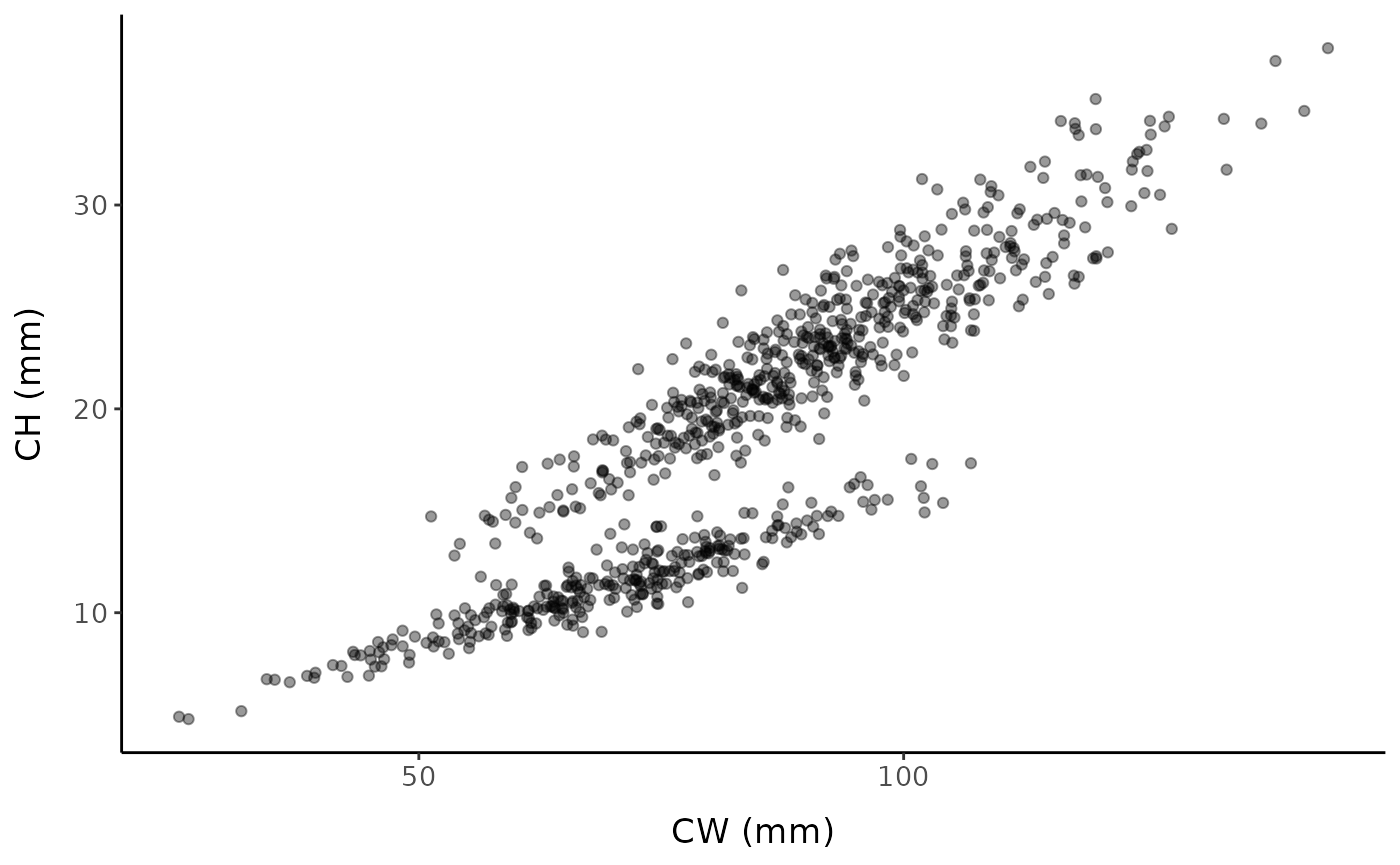
We will start by simulating a data set with a known SM50 value of 75 mm to demonstrate the use (and limitations) of broken-stick methods.
set.seed(12) # set seed for reproducibility
fc <- fake_crustaceans(
error_scale = 17,
slope = 9,
L50 = 75, # known size at maturity is 75 mm
n = 800, # sample size
allo_params = c(0.9, 0.25, 1.05, 0.2),
x_mean = 85 # mean carapace width of the sample
)
segmented package
A powerful and customizable method of implementing broken-stick
regression is provided by the R package segmented, which
has been cited by many papers using morphometric data to estimate size
at maturity. Note that segmented includes three different
methods to compute confidence intervals, the details of which are
discussed in Muggeo (2017). It is also possible to estimate
95% CIs via bootstrap resampling, but the computation time required is
relatively high and the resulting estimates are around the same values
as those from the “delta” and “gradient” methods included in the
segmented package.
The segmented package has three built-in methods to get 95% confidence intervals for the break point:
#> Delta method:#> Est. CI(95%).low CI(95%).up
#> psi1.x 63.9545 57.1425 70.7665#> Score method:#> Est. CI(95%).low CI(95%).up
#> psi1.x 63.9545 50.1308 67.6307#> Gradient method:#> Est. CI(95%).low CI(95%).up
#> psi1.x 63.9545 53.7911 70.2144We can also use an ANOVA test to compare the segmented model to a single linear model:
anova(lm_orig, lm_orig_seg)#> Analysis of Variance Table
#>
#> Model 1: y ~ x
#> Model 2: y ~ x + U1.x + psi1.x
#> Res.Df RSS Df Sum of Sq F Pr(>F)
#> 1 798 7866.2
#> 2 796 7629.8 2 236.4 12.332 5.318e-06 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1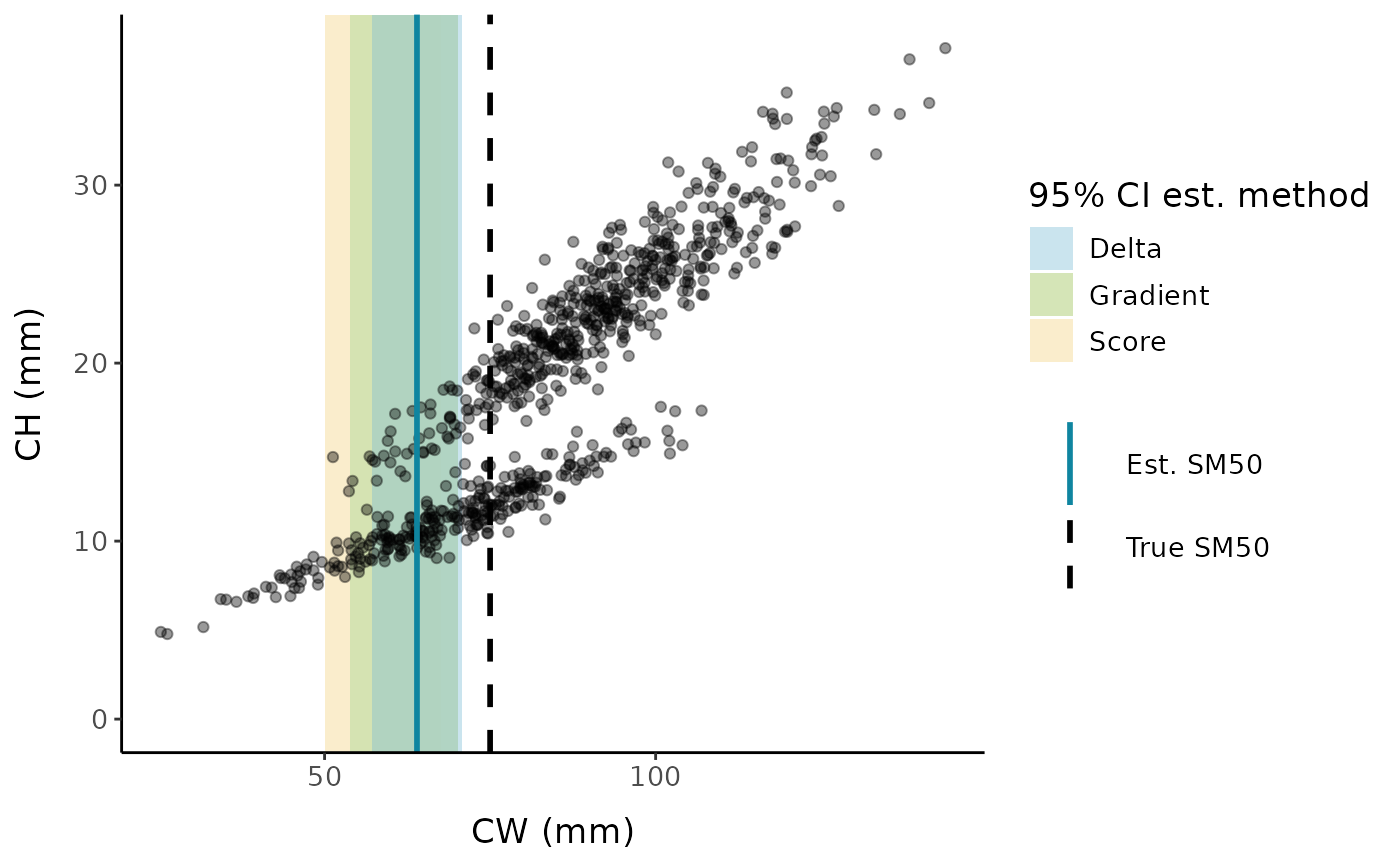
SM50 estimate for simulated crab data from the R package segmented
chngpt package
Another R package with the capability of segmented regression is
called chngpt. This package differs slightly from
segmented in the types of threshold models that are
supported, the optimization algorithms used for parameter estimation,
and the method(s) used to calculate confidence intervals for the
breakpoint (Fong et al.
2017).
fit_chngpt <- chngptm(
formula.1 = y ~ 1,
formula.2 = ~ x,
family = "gaussian",
data = fc,
type = "segmented",
var.type = "default",
weights = NULL
)
summary(fit_chngpt)
#> Change point model threshold.type: segmented
#>
#> Coefficients:
#> est Std. Error* (lower upper) p.value*
#> (Intercept) -0.9153689 0.62858364 -1.9643531 0.4996948 1.453262e-01
#> x 0.2005470 0.01357774 0.1688772 0.2221020 2.277627e-49
#> (x-chngpt)+ 0.1425691 0.01659954 0.1134477 0.1785179 8.793325e-18
#>
#> Threshold:
#> est Std. Error (lower upper)
#> 63.954507 2.031396 58.890638 66.853710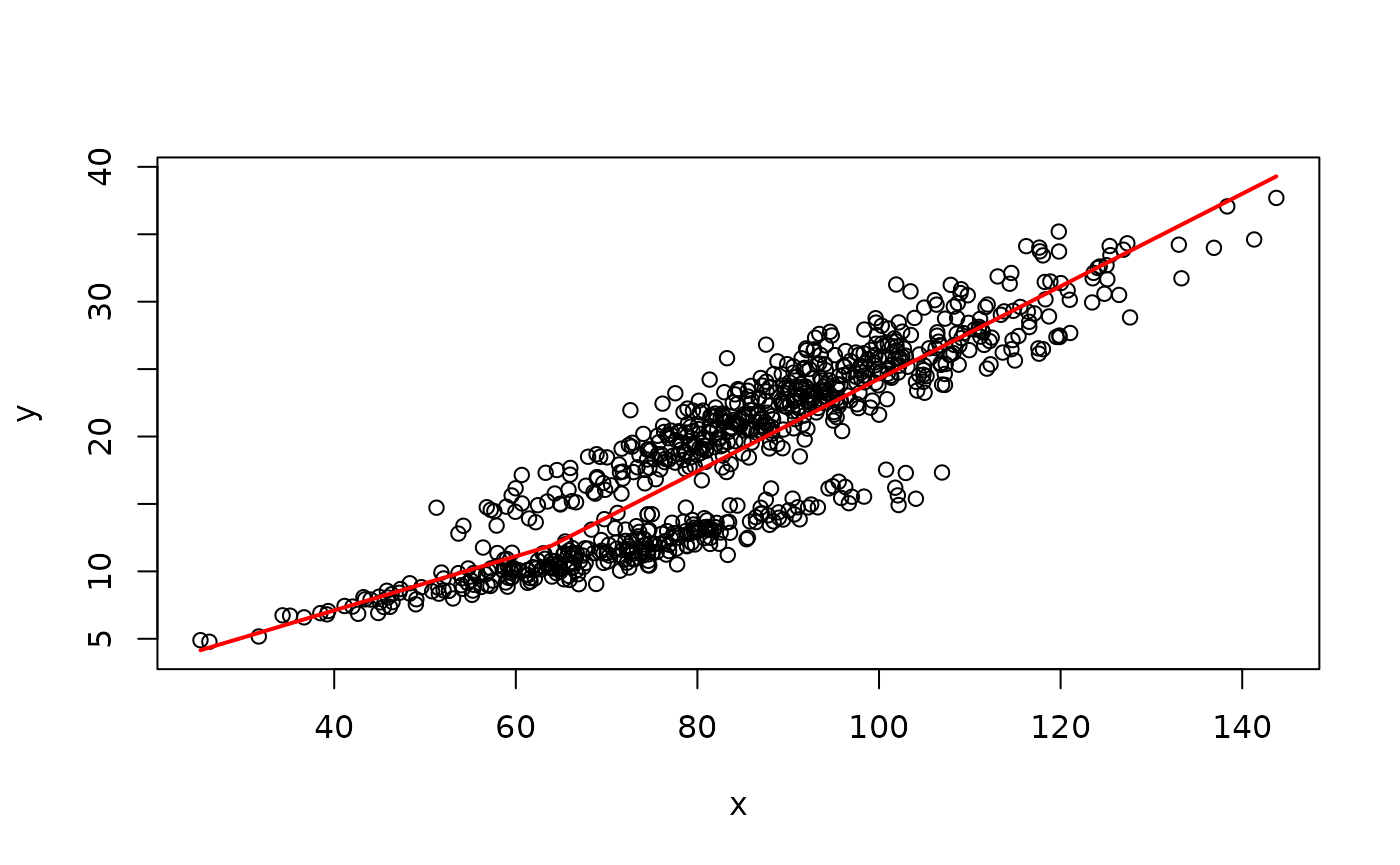
Broken-stick model from the package chngpt

Log likelihood of the model at various breakpoint values
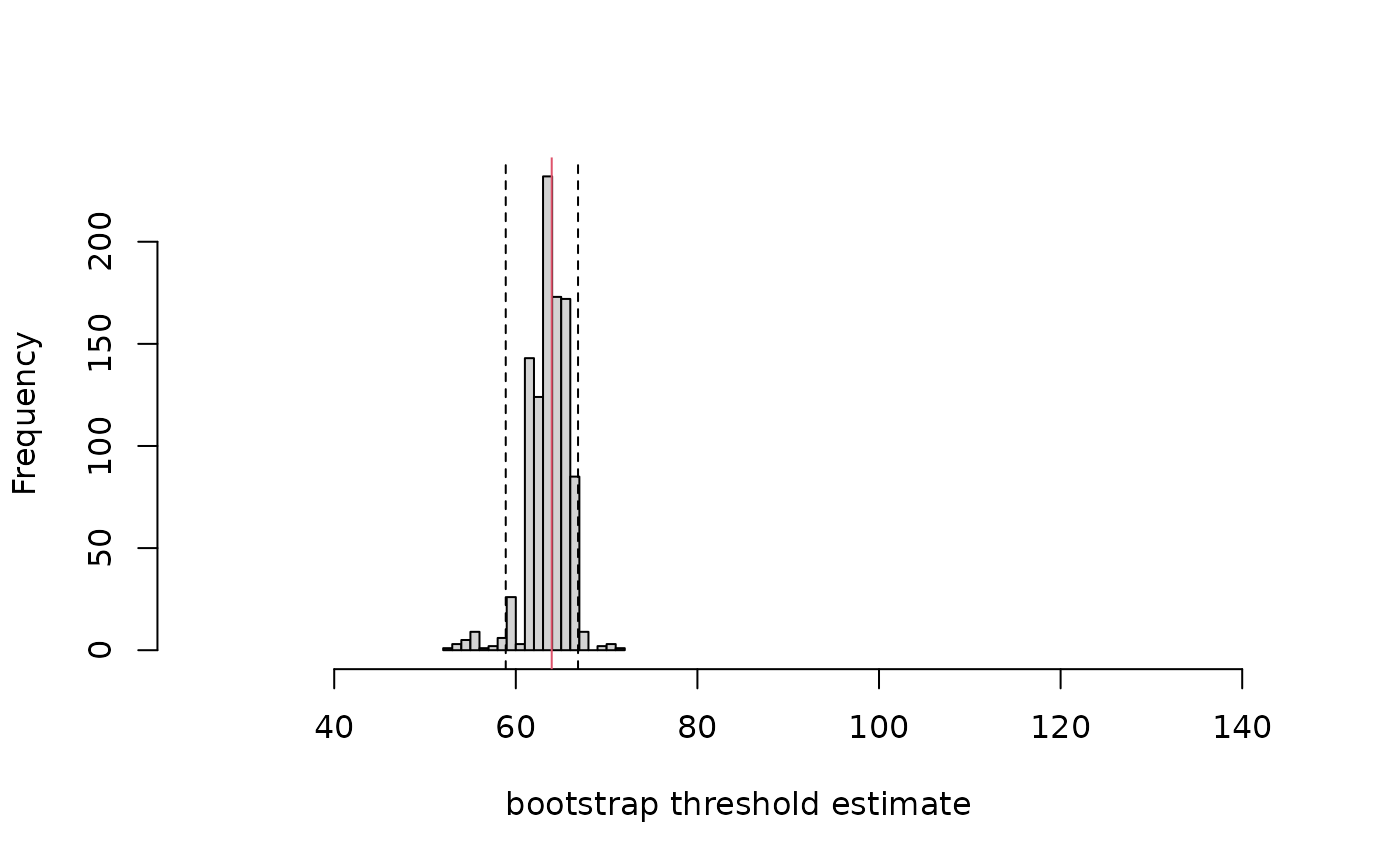
Bootstrap 95% confidence intervals
As with the segmented package, it seems to have
significantly underestimated SM50 compared to the true value of 75,
which is not contained within the bootstrap confidence intervals. An
alternative method for calculating confidence intervals (“model-based”)
produces very similar results to the default bootstrap method.
summary(
chngptm(
formula.1 = y ~ 1,
formula.2 = ~ x,
family = "gaussian",
data = fc,
type = "segmented",
var.type = "model", # note change from default to model
weights = NULL
)
)[["chngpt"]]
#> est Std. Error (lower upper)
#> 63.954507 3.364602 55.814677 69.003917Adding a starting breakpoint value of 75 (i.e., initializing the search at the correct value) through the “chngpt.init” argument does not affect the estimate, although it does result in narrower confidence intervals:
summary(
chngptm(
formula.1 = y ~ 1,
formula.2 = ~ x,
family = "gaussian",
data = fc,
type = "segmented",
chngpt.init = 75,
weights = NULL
)
)[["chngpt"]]#> est Std. Error (lower upper)
#> 63.954507 2.031396 58.890638 66.853710This method is EXTREMELY sensitive to the “lb.quantile” and “ub.quantile” arguments, which refer to the lower and upper bounds of the search range for change point estimate, respectively (the function defaults are 0.05 and 0.95). For example, if we change the lower quantile bound to 0.33 and the upper to 0.66, the model will return an SM50 value closer to the true value of 75 mm.
summary(
chngptm(
formula.1 = y ~ 1,
formula.2 = ~ x,
family = "gaussian",
data = fc,
type = "segmented",
var.type = "model",
lb.quantile = 0.33,
ub.quantile = 0.66,
weights = NULL
)
)[["chngpt"]][1]#> est
#> 76.00473The estimates and accuracy also change dramatically even with slightly different variations of data with the exact same underlying structure. Results from detailed investigations of the sensitivity of each modeling approach will be available in a forthcoming paper (Krasnow et al., in prep).
Although we will not test all of the options here, the
chngpt package supports 14 different types of two-phase
(one threshold) models, as well as one three-phase model: see Fig. 1
in Son and Fong (2021). Importantly, it also supports
generalized linear models and linear mixed models, so you can fit models
utilizing any family that can be passed to glm and include
other covariates and random effects. Additional benefits of this package
include several functions to simulate data and the significant
capability of user-friendly customization. Options include providing
your own grid of changepoints to iterate over, using five different
types of bootstrap CIs with numerous options for each type, providing a
bound on the slope parameters for the lines on either side of the
breakpoint, and changing the search/optimization algorithm for parameter
estimation to meet the needs of your data (e.g., “fastgrid2” is very
fast and might be helpful for large data sets).
Using the chngpt::chngpt.test() function to run
significance tests:
# Model with default upper and lower bounds
chngpt.test(
formula.null = y ~ 1,
formula.chngpt = ~ x,
family = "gaussian",
data = fc,
type = "segmented"
)
#>
#> Maximum of Likelihood Ratio Statistics
#>
#> data: fc
#> Maximal statistic = 24.358, threshold = 64.292, p-value < 2.2e-16
#> alternative hypothesis: two-sided
# Model with better upper and lower bounds to return
# the true SM50 of 75 mm (0.6 and 0.3)
chngpt.test(
formula.null = y ~ 1,
formula.chngpt = ~ x,
family = "gaussian",
data = fc,
type = "segmented",
lb.quantile = 0.3,
ub.quantile = 0.6
)
#>
#> Maximum of Likelihood Ratio Statistics
#>
#> data: fc
#> Maximal statistic = 13.909, threshold = 74.531, p-value = 0.00036
#> alternative hypothesis: two-sidedIt is interesting that this function returns a slightly different
breakpoint/threshold estimate from the chngpt::chngptm()
function when both are called using the default search region bounds
(regardless of what set.seed is set to before calling the functions).
Additionally, the test statistic for the model with the less accurate
breakpoint estimate is much higher than for the more accurate model,
yielding a lower p-value.
REGRANS
We will also test the broken-stick method by manually coding an algorithm to identify the appropriate breakpoint. The following code is conceptually very similar to the R version of REGRANS, which was initially written in 1993 in the programming language BASIC (pezzuto1993?).
You can optionally define lower and upper limits for the changepoints you want this function to test; otherwise, it tests a user-defined number of evenly-spaced values (default = 100) ranging from the 0.2 quantile to the 0.8 quantile of the x-axis variable.
regrans_est <- regrans(fc, "x", "y", verbose = FALSE)
regrans_est#> [1] 67.67091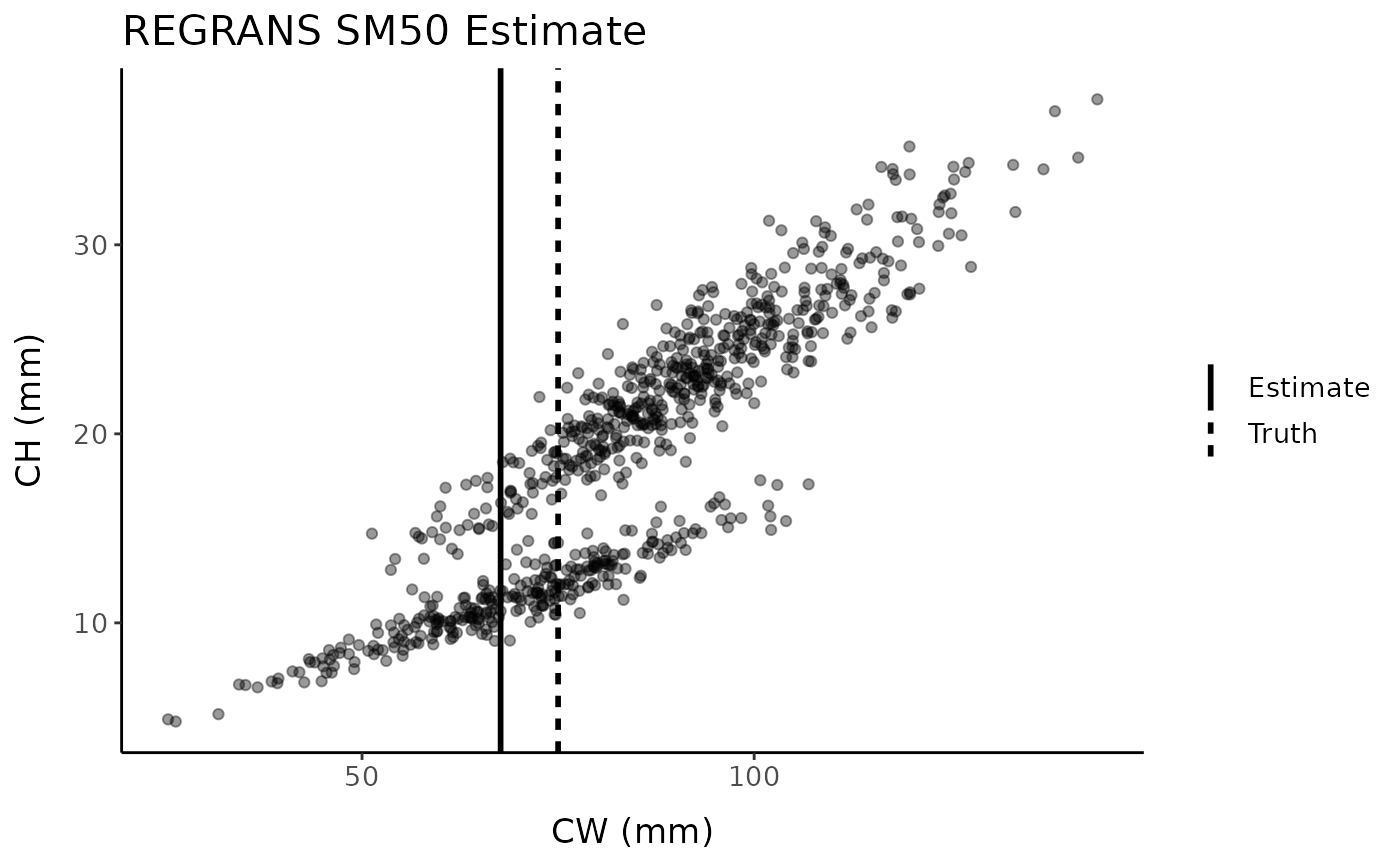
As with the previous broken-stick methods, REGRANS tends to underestimate SM50 and the model estimates are highly sensitive to the values of the upper and lower bounds of the region considered plausible to contain the SM50 value.
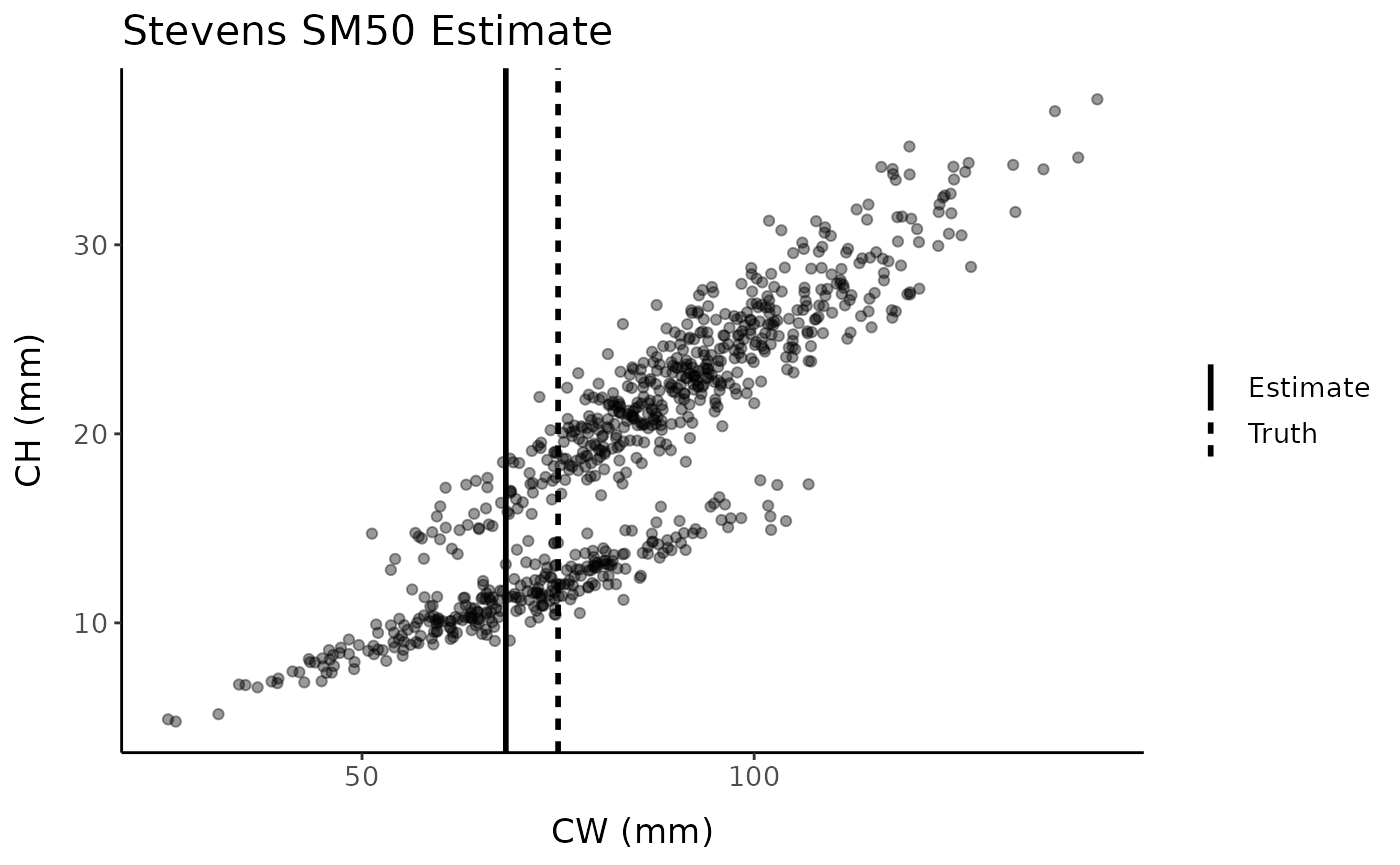
Crab_Maturity Type A (Broken-stick Stevens)
A third algorithm for using segmented regression to estimate SM50 was
written by Dr. Bradley Stevens at the University of Maryland Eastern
Shore. This code is part of the Crab_Maturity
program available on GitHub. There are several different methods
included within Crab_Maturity; this segmented regression approach is
included here because it differs from the segmented and
REGRANS methods in that possible SM50 values are restricted to
values of the x-variable present in the data set.
See Olsen and Stevens (2020) for an example real-world application.
stevens_est <- broken_stick_stevens(fc, "x", "y", verbose = FALSE)
stevens_est#> [1] 68.33387