set.seed(12) # set seed for reproducibility
fc <- fake_crustaceans(
error_scale = 17,
slope = 9,
L50 = 75, # known size at maturity is 75 mm
n = 800, # sample size
allo_params = c(0.9, 0.25, 1.05, 0.2),
x_mean = 85 # mean carapace width of the sample
)
clust_dat <- cbind(fc$x, fc$y)
mclust_class <- mclust::Mclust(data = clust_dat,
G = 2,
modelNames = "EVV")
fc_mclust <- fc %>%
rename(true_maturity = mature) %>%
mutate(pred_maturity = mclust_class$classification)
mature_label <- slice_max(fc_mclust, x) %>% pull(pred_maturity)
fc_mclust <- fc_mclust %>%
mutate(
pred_maturity = if_else(pred_maturity == mature_label,
as.factor(1),
as.factor(0)),
pred_maturity_num = if_else(pred_maturity == 1,
as.numeric(1),
as.numeric(0))) %>%
mutate(uncertainty = mclust_class$uncertainty)Post-classification logistic regression
Beyond the familiar stats::glm, there are many packages
that can be used to model the relationship between size and maturity
status, allowing for the incorporation of random effects, temporal or
spatial structuring, and other additional complexities. These include
popular packages for fitting generalized linear mixed models (GLMMs) and
generalized additive (mixed) models (GAMMs) such as lmer,
nlme, mgcv, glmmTMB, and
sdmTMB. While logit links are the most common for binomial
models like these, testing alternative link functions—particularly the
probit and complementary log-log (“cloglog”) links—may be important for
ensuring reliable parameter estimates (Mainguy et al. 2024). Also see Roa et
al. (1999).
Helpful vignette: https://cran.r-project.org/web/packages/qra/vignettes/timeMortality.html
Even if no covariates are included in the model, many choices must be made when fitting a binomial model for the probability of maturity at a given length. These include:
- The model to be fitted (most commonly 2-parameter logistic models, but many alternative formulations with up to 5 parameters)
- Alternative link functions (logit, probit, cloglog, etc.)
- Constrained optimization (i.e., set lower and upper bounds on the possible values of the parameters to be estimated)
- Initial values provided for the parameters to be estimated
Example methods to obtain confidence intervals for SM50 value
A great place to start is the confint_L.R script from Mainguy et al. (2024). This script can be used to quantify the uncertainty around the SM50 parameter using the Delta method, Fieller method, profile-likelihood, three resampling techniques (non-parametric bootstrapping, parametric bootstrapping, and Monte Carlo), and Bayesian credible intervals. For the resampling methods, three types of intervals can be calculated: equal-tailed intervals (ETI/percentile), bias corrected accelerated intervals (BCa), or highest density intervals (HDI).
Standard glm
example_glm <- glm(data = fc_mclust,
pred_maturity_num ~ x,
family = binomial(link = "logit"))
broom::tidy(example_glm, conf.int = TRUE)#> # A tibble: 2 × 7
#> term estimate std.error statistic p.value conf.low conf.high
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) -7.76 0.615 -12.6 1.54e-36 -9.01 -6.60
#> 2 x 0.104 0.00772 13.4 4.63e-41 0.0891 0.119
broom::glance(example_glm) %>%
dplyr::select(-c(null.deviance, df.null)) %>%
mutate(across(where(is.double), ~ round(.x, digits = 2)))#> # A tibble: 1 × 6
#> logLik AIC BIC deviance df.residual nobs
#> <dbl> <dbl> <dbl> <dbl> <int> <int>
#> 1 -352. 708. 718. 704. 798 800drc package
The R package drc was designed for analysis of dose-response data, and includes many functions that are useful for fitting logistic models (Ritz et al. 2015). This package can fit a variety of 5/4/3/2-parameter logistic, log-logistic, and Weibull models and find confidence intervals for the estimated parameters, among other functions.
testdrm <- drc::drm(pred_maturity_num ~ x,
data = fc_mclust,
fct = LL.2(),
type = "binomial")
testdrm#>
#> A 'drc' model.
#>
#> Call:
#> drc::drm(formula = pred_maturity_num ~ x, data = fc_mclust, fct = LL.2(), type = "binomial")
#>
#> Coefficients:
#> b:(Intercept) e:(Intercept)
#> -7.996 74.001
summary(testdrm)#>
#> Model fitted: Log-logistic (ED50 as parameter) with lower limit at 0 and upper limit at 1 (2 parms)
#>
#> Parameter estimates:
#>
#> Estimate Std. Error t-value p-value
#> b:(Intercept) -7.99575 0.59870 -13.355 < 2.2e-16 ***
#> e:(Intercept) 74.00087 0.93113 79.475 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
confint(testdrm, "e") # specifies the 'e' parameter, the inflection point#> 2.5 % 97.5 %
#> e:(Intercept) 72.1759 75.82584
estfun.drc <- drc::estfun.drc
bread.drc <- drc::bread.drc
# use lmtest and sandwich packages to obtain robust standard errors
lmtest::coeftest(testdrm, vcov = sandwich) #>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> b:(Intercept) -7.99575 0.60852 -13.140 < 2.2e-16 ***
#> e:(Intercept) 74.00087 0.96722 76.508 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#>
#> Estimated effective doses
#>
#> Estimate Std. Error Lower Upper
#> e:1:50 74.00087 0.93113 72.17590 75.82584
plot(testdrm) # built-in plotting method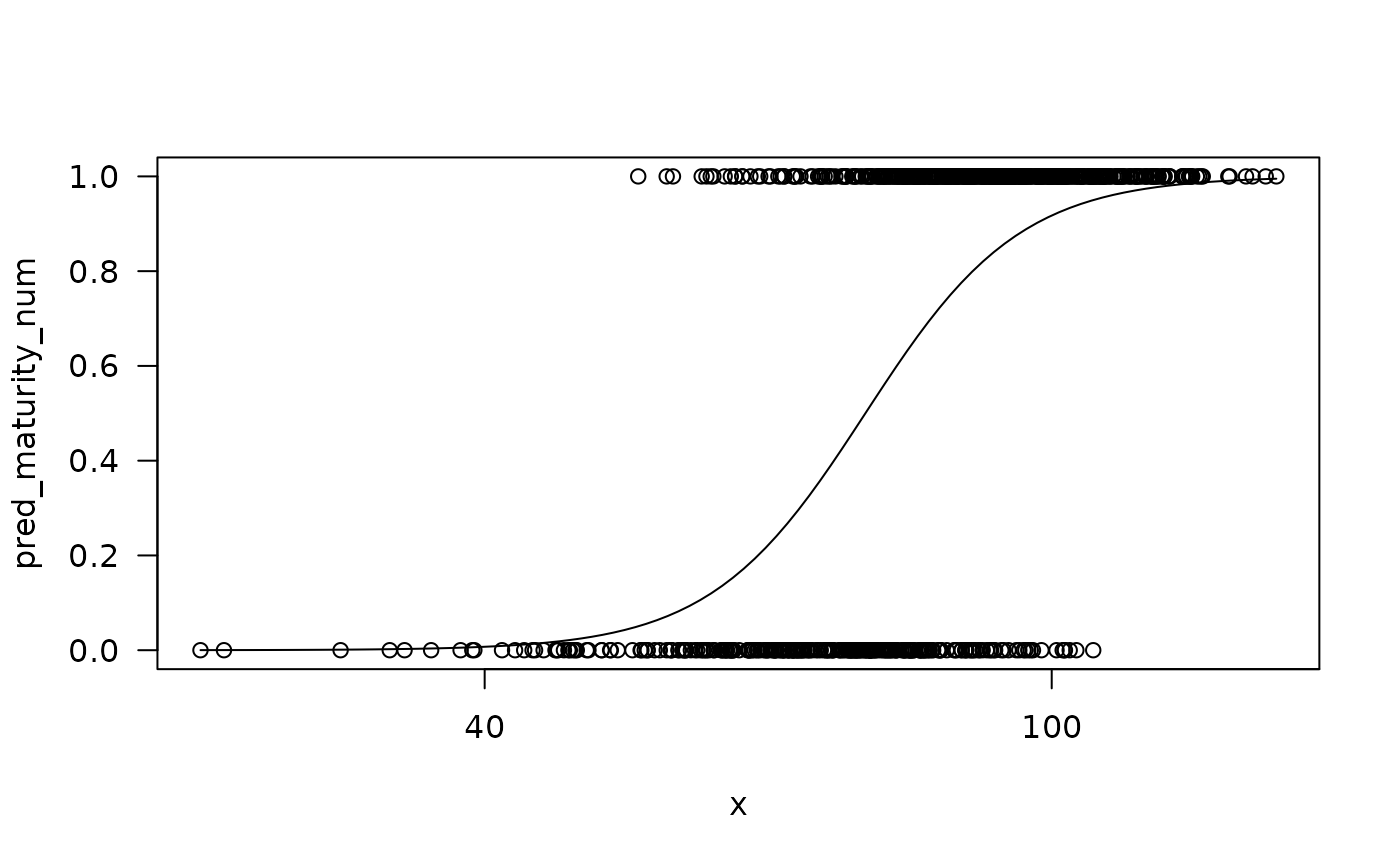
Custom plot example:
sm50_est <- coef(testdrm)[2]
low_ci <- confint(testdrm, "e")[1]
hi_ci <- confint(testdrm, "e")[2]
ggplot() +
geom_point(aes(x = fc_mclust$x, y = fc_mclust$pred_maturity_num),
shape = 1, size = 1) +
geom_line(aes(x = fc_mclust$x, y = predict(testdrm))) +
geom_vline(xintercept = sm50_est) +
geom_rect(aes(xmin = low_ci, xmax = hi_ci,
ymin = -Inf, ymax = Inf, fill = "95% CI"), alpha = 0.5) +
labs(y = "Probability of maturity", x = "Carapace width (mm)", fill = NULL) +
mytheme +
theme(legend.position = "inside", legend.position.inside = c(0.75, 0.25))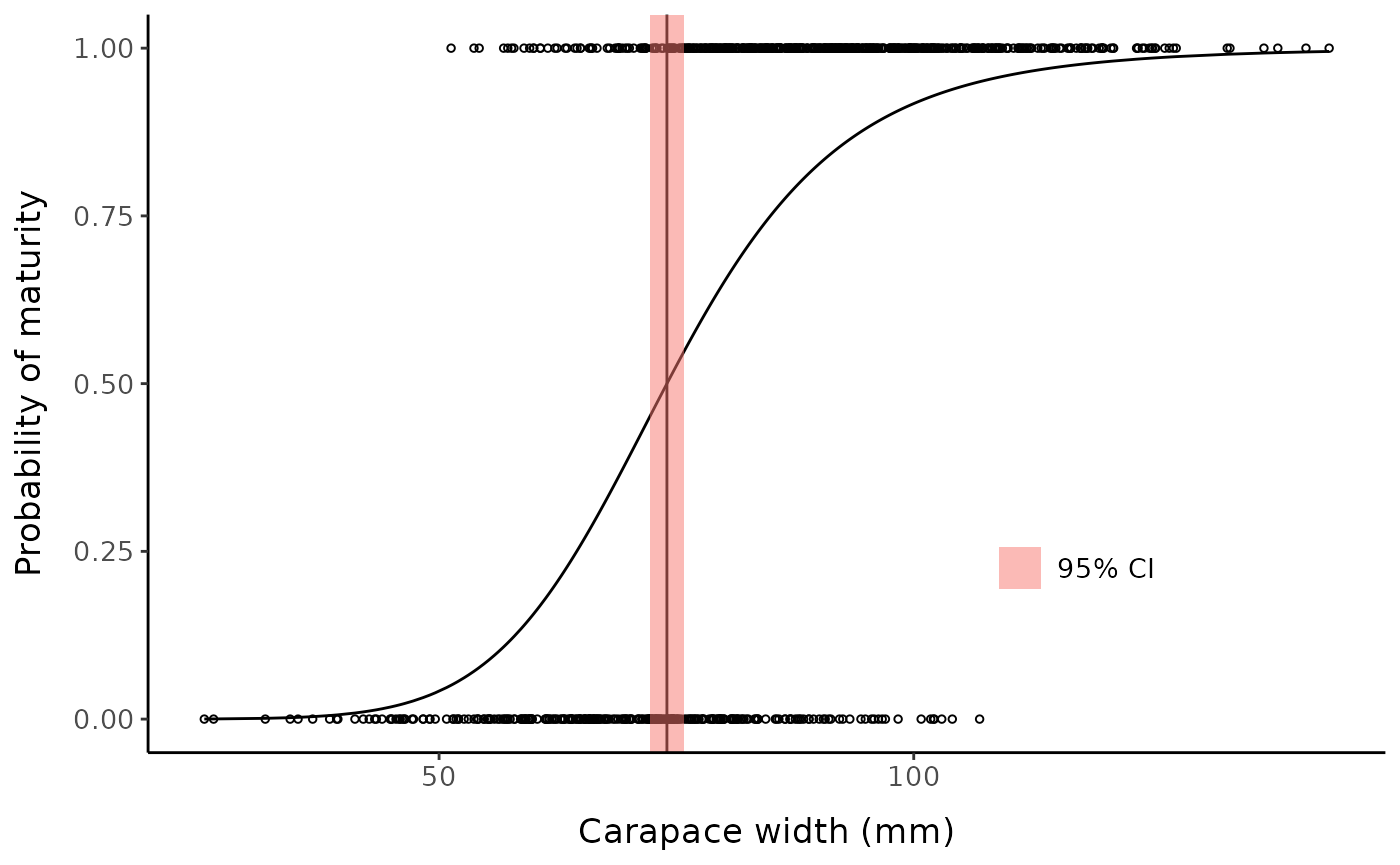
DRDA package
The R package DRDA is a newer alternative to drc that uses an improved optimization methodology to improve the accuracy of parameter estimates (Malyutina, Tang, and Pessia 2023).
fit_l2 <- drda(pred_maturity_num ~ x,
data = fc_mclust,
mean_function = "logistic2")
fit_l4 <- drda(pred_maturity_num ~ x,
data = fc_mclust,
mean_function = "logistic4")
anova(fit_l2, fit_l4)#> Analysis of Deviance Table
#>
#> Model 1: a
#> Model 2: 1 / (1 + exp(-e * (x - p)))
#> Model 3: a + d / (1 + exp(-e * (x - p)))
#> Model 4: a + d / (1 + n * exp(-e * (x - p)))^(1 / n) (Full)
#>
#> Model 2 is the best model according to the Akaike Information Criterion.
#>
#> Resid. Df Resid. Dev Df AIC BIC Deviance LRT Pr(>Chi)
#> Model 1 799 184.04 1098.73 1108.10
#> Model 2 798 114.59 1 721.74 735.79 -69.443 378.99 <2e-16 ***
#> Model 3 796 114.50 2 725.11 748.53 -0.091 0.63 0.7290
#> Model 4 795 114.39 1 726.33 754.44 -0.111 0.78 0.3783
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(fit_l2)#>
#> Call: drda(formula = pred_maturity_num ~ x, data = fc_mclust, mean_function = "logistic2")
#>
#> Pearson Residuals:
#> Min 1Q Median 3Q Max
#> -2.5524 -0.5319 0.1131 0.5676 2.4444
#>
#> Parameters:
#> Estimate Std. Error Lower .95 Upper .95
#> Minimum 0.0000 NA NA NA
#> Height 1.0000 NA NA NA
#> Growth rate 0.1063 0.009468 0.0877 0.125
#> Midpoint at 75.0850 0.802979 73.5112 76.659
#> Residual std err. 0.3790 0.009492 0.3603 0.398
#>
#> Residual standard error on 798 degrees of freedom
#>
#> Log-likelihood: -357.87
#> AIC: 721.74
#> BIC: 735.79
#>
#> Optimization algorithm converged in 291 iterations
plot(fit_l2) # built-in plotting method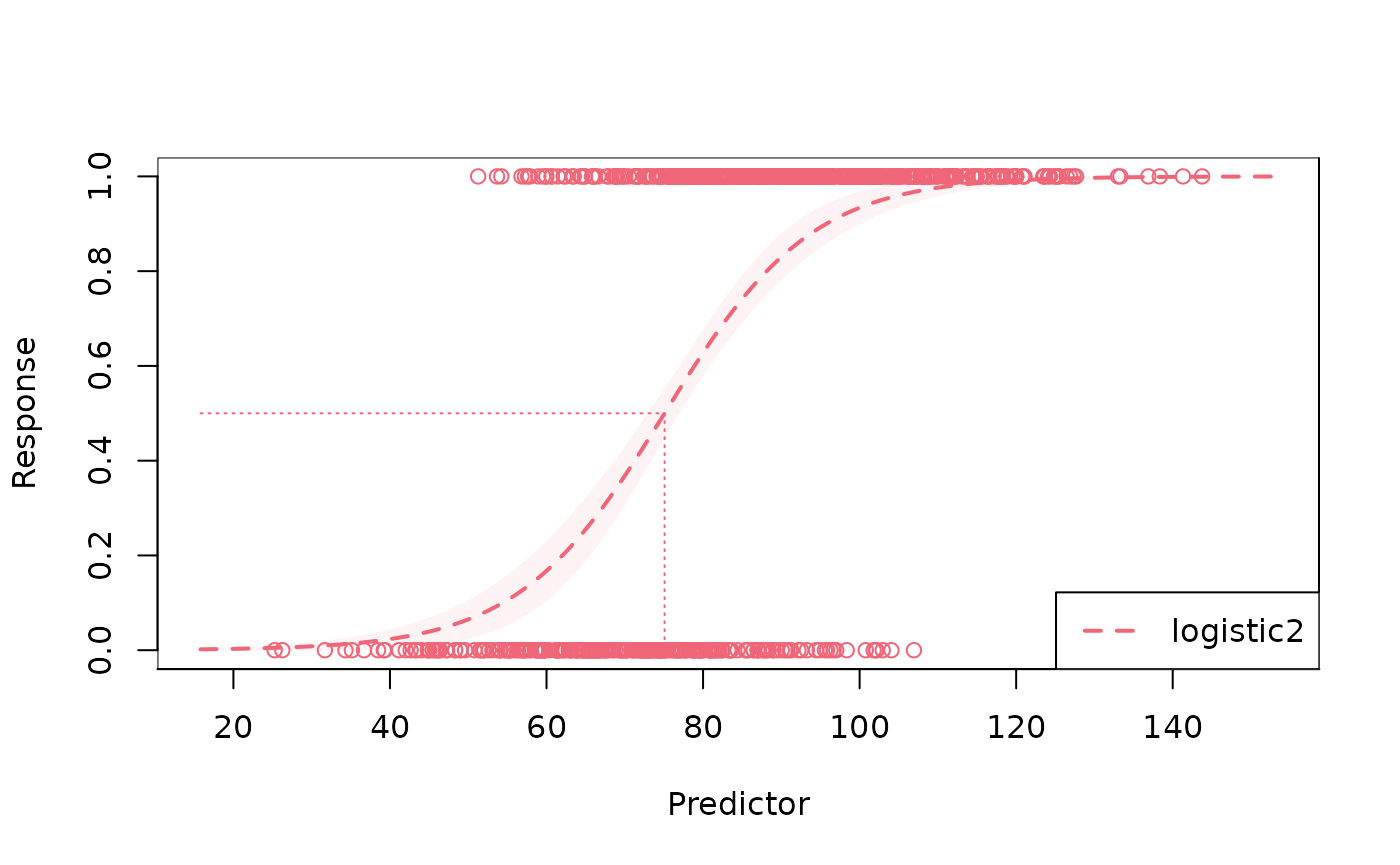
Custom plot example:
sum_l2 <- summary(fit_l2)[["param"]][4,]
sm50_est <- sum_l2[1]
low_ci <- sum_l2[3]
hi_ci <- sum_l2[4]
ggplot() +
geom_point(aes(x = fc_mclust$x, y = fc_mclust$pred_maturity_num),
shape = 1, size = 1) +
geom_line(aes(x = fc_mclust$x, y = predict(fit_l2))) +
geom_vline(xintercept = sm50_est) +
geom_rect(aes(xmin = low_ci, xmax = hi_ci,
ymin = -Inf, ymax = Inf, fill = "95% CI"), alpha = 0.5) +
labs(y = "Probability of maturity", x = "Carapace width (mm)", fill = NULL) +
mytheme +
theme(legend.position = "inside", legend.position.inside = c(0.75, 0.25))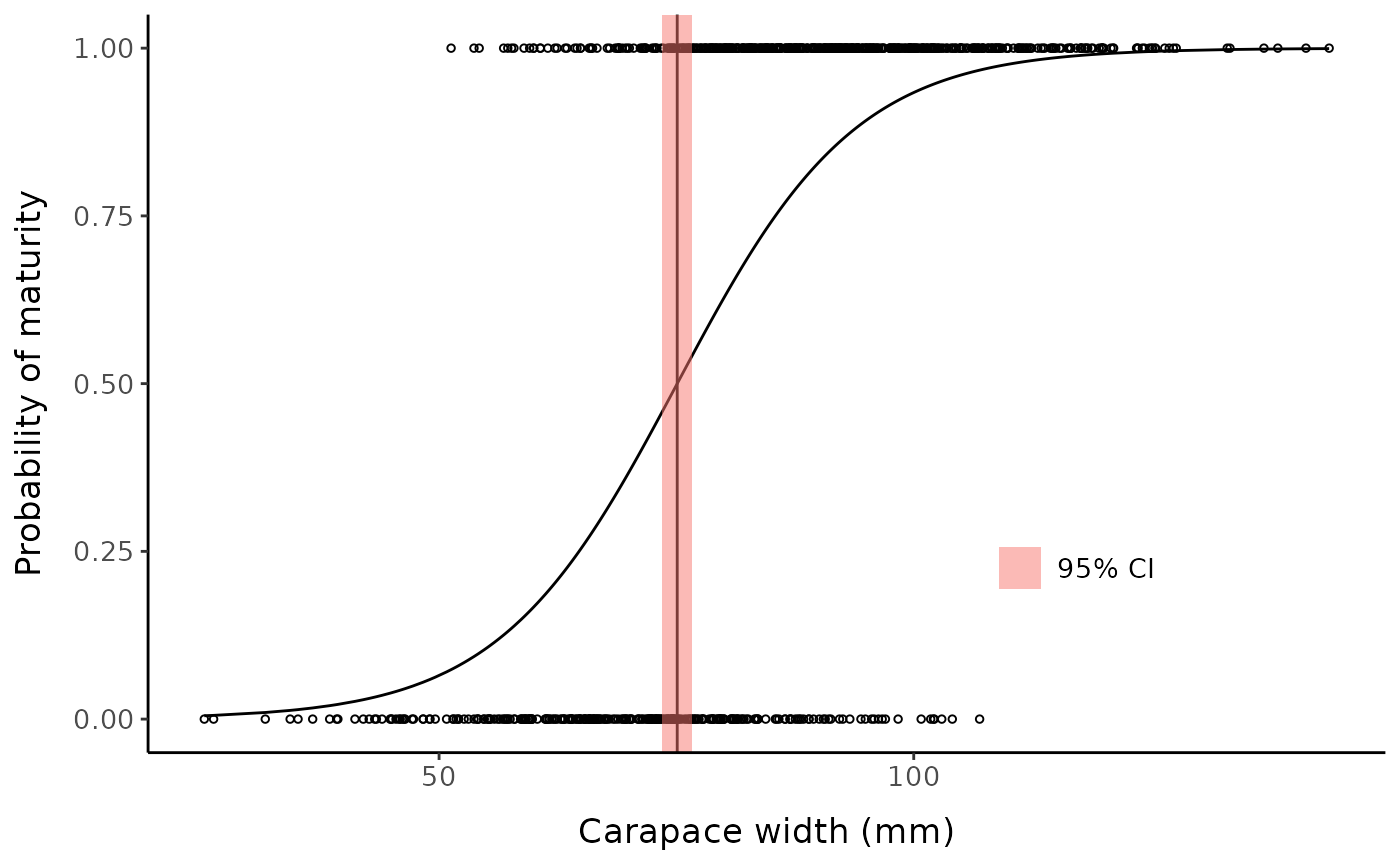
qra package
The R package qra is
another useful package initially designed for analyzing dose-response
data (Maindonald
2021). It includes implementations of the the Fieller and
Delta methods for estimating confidence intervals for the SM50 parameter
when it is not directly estimated during model-fitting. See
qra::fieller() for details of usage and outputs.
#> est var lwr upr g
#> 74.8902398 0.8919419 72.9346488 76.6805775 0.0213313
qra::fieller(
0.5,
b = coef(example_glm),
vv = vcov(example_glm),
type = "Delta" # probably OK because of low g value
)#> est var lwr upr g
#> 74.8902398 0.8919419 73.0391634 76.7413162 0.0000000Custom plot example:
qra_est <- qra::fieller(
0.5,
b = coef(example_glm),
vv = vcov(example_glm),
type = "Fieller"
)
sm50_est <- qra_est[1]
low_ci <- qra_est[3]
hi_ci <- qra_est[4]
ggplot() +
geom_point(aes(x = fc_mclust$x, y = fc_mclust$pred_maturity_num),
shape = 1, size = 1) +
geom_line(aes(x = fc_mclust$x, y = predict(example_glm, type = "response"))) +
geom_vline(xintercept = sm50_est) +
geom_rect(aes(xmin = low_ci, xmax = hi_ci,
ymin = -Inf, ymax = Inf, fill = "95% CI"), alpha = 0.5) +
labs(y = "Probability of maturity", x = "Carapace width (mm)", fill = NULL) +
mytheme +
theme(legend.position = "inside", legend.position.inside = c(0.75, 0.25))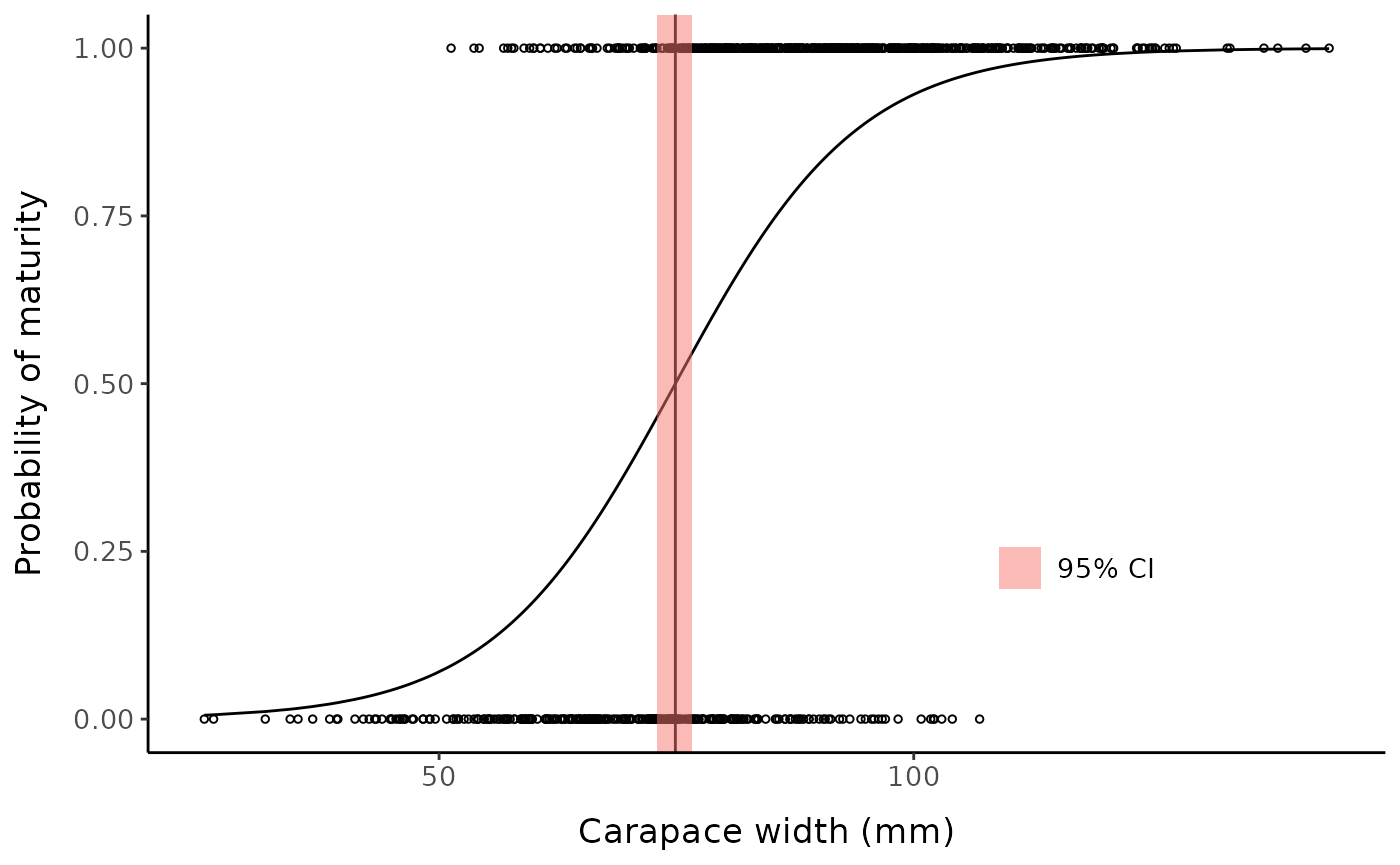
Others
Other functions that could be used (that I have not tested) include
twopartm::FiellerRatio()
and tidydelta::tidydelta().
