This vignette describes methods that first classify individual data points as mature or immature, enabling the use of logistic regression to find SM50 as would be done with a physiological metric of maturity.
This is the approach taken by the classify_mature()
function in the sizeMat
package, which first applies PCA to the allometric data, then uses
hierarchical clustering (with the “Ward.D” agglomeration method and a
standard Euclidean distance metric) to classify points as mature or
immature. Simulation testing demonstrated that Gaussian mixture model
clustering is generally more accurate at recovering true maturity
classifications than hierarchical clustering, kmeans clustering,
hierarchical kmeans, or partitioning around medoids (PAM) clustering.
However, morphmat includes all clustering methods to allow users to
easily compare results and identify how the choice of clustering method
may impact the results of their analysis.
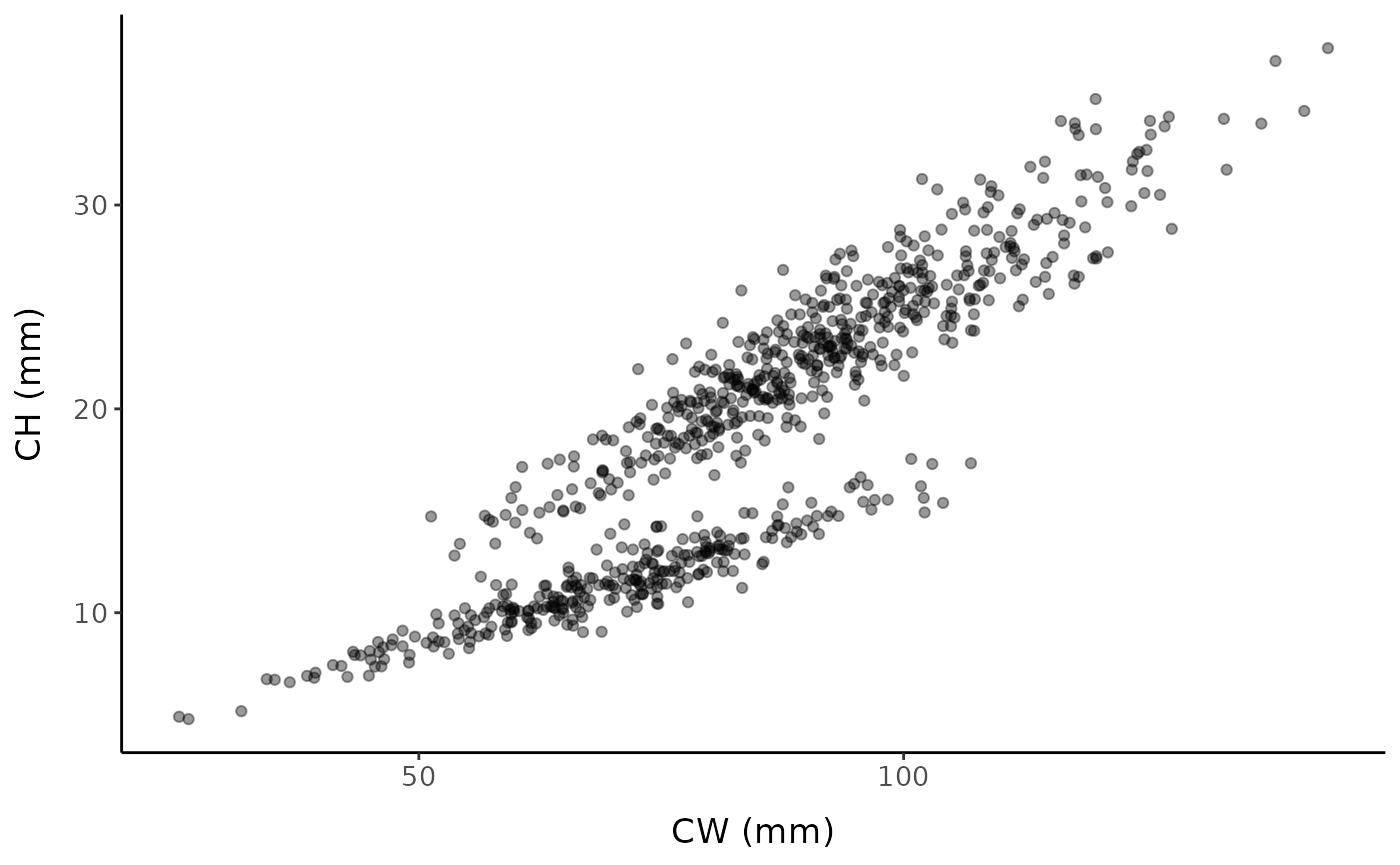
We will start by simulating a data set with a known SM50 value of 75 mm:
set.seed(12) # set seed for reproducibility
fc <- fake_crustaceans(
error_scale = 17,
slope = 9,
L50 = 75, # known size at maturity is 75 mm
n = 800, # sample size
allo_params = c(0.9, 0.25, 1.05, 0.2),
x_mean = 85 # mean carapace width of the sample
)
Clustering methods
Innumerable clustering methods have been implemented in existing R
packages. I will be using simulation testing to evaluate the relative
performance of common clustering methods when used to separate immature
and mature crustaceans based on morphometric data. Functions included in
the simulation testing will include hclust() and
kmeans() from the base R stats package;
factoextra::hkmeans(); cluster::PAM();
mclust::Mclust(); and dbscan(),
hdbscan(), and OPTICS() from the
dbscan package.
The Somerton method is a clustering method widely used for estimating
size at maturity based on the allometric growth of crustacean body
parts, originally written in FORTRAN (Somerton 1980).
morphmat contains code to implement the Somerton method in
R, largely following the structure of code written by Dr. Bradley
Stevens.
Somerton method
somerton_out <- somerton(fc, xvar = "x", yvar = "y")
out_df <- somerton_out[[1]]
juv_int <- somerton_out$juv_mod$coefficients[[1]]
juv_slope <- somerton_out$juv_mod$coefficients[[2]]
mat_int <- somerton_out$adult_mod$coefficients[[1]]
mat_slope <- somerton_out$adult_mod$coefficients[[2]]
ggplot() +
geom_point(data = out_df, aes(x, y, color = as.factor(pred_mat_num)),
alpha = 0.4) +
labs(x = "CW (mm)", y = "CH (mm)", color = "Predicted maturity") +
scale_color_manual(
values = c("0" = "#7bbcd5", "1" = "#CA6E78"),
breaks = c(0, 1),
labels = c("0" = "Immature", "1" = "Mature")) +
geom_abline(slope = juv_slope, intercept = juv_int, color = "#7bbcd5") +
geom_abline(slope = mat_slope, intercept = mat_int, color = "#CA6E78") +
mytheme +
annotate("text", x = c(120, 120), y = c(8, 6),
label = c(
sprintf("y[1] == %.3g + %.3g * x", juv_int, juv_slope),
sprintf("y[2] == %.3g + %.3g * x", mat_int, mat_slope)),
parse = TRUE)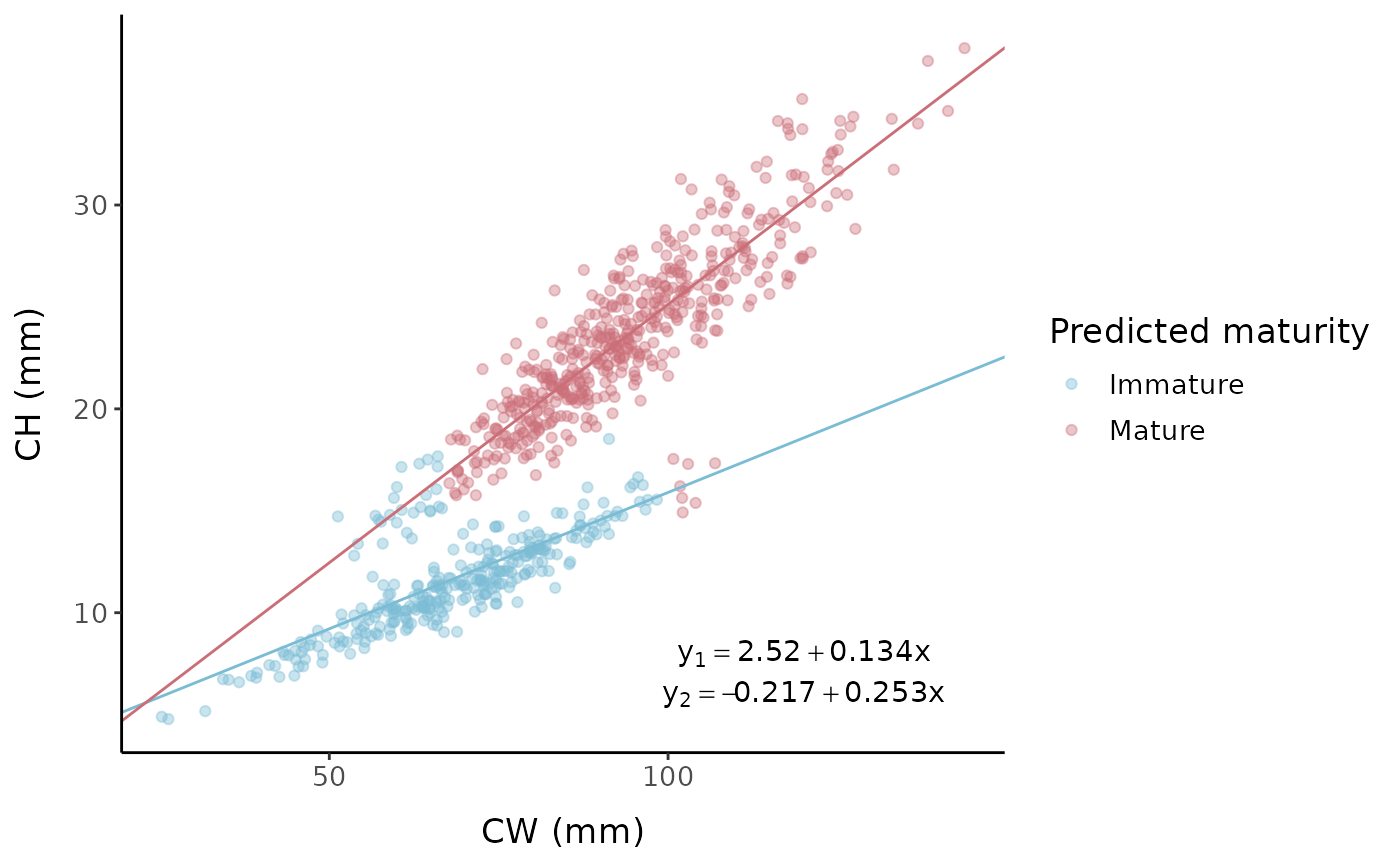
Other classification methods
Inflection point discriminant method
disc <- infl_pt(fc, "x", "y", plot = TRUE)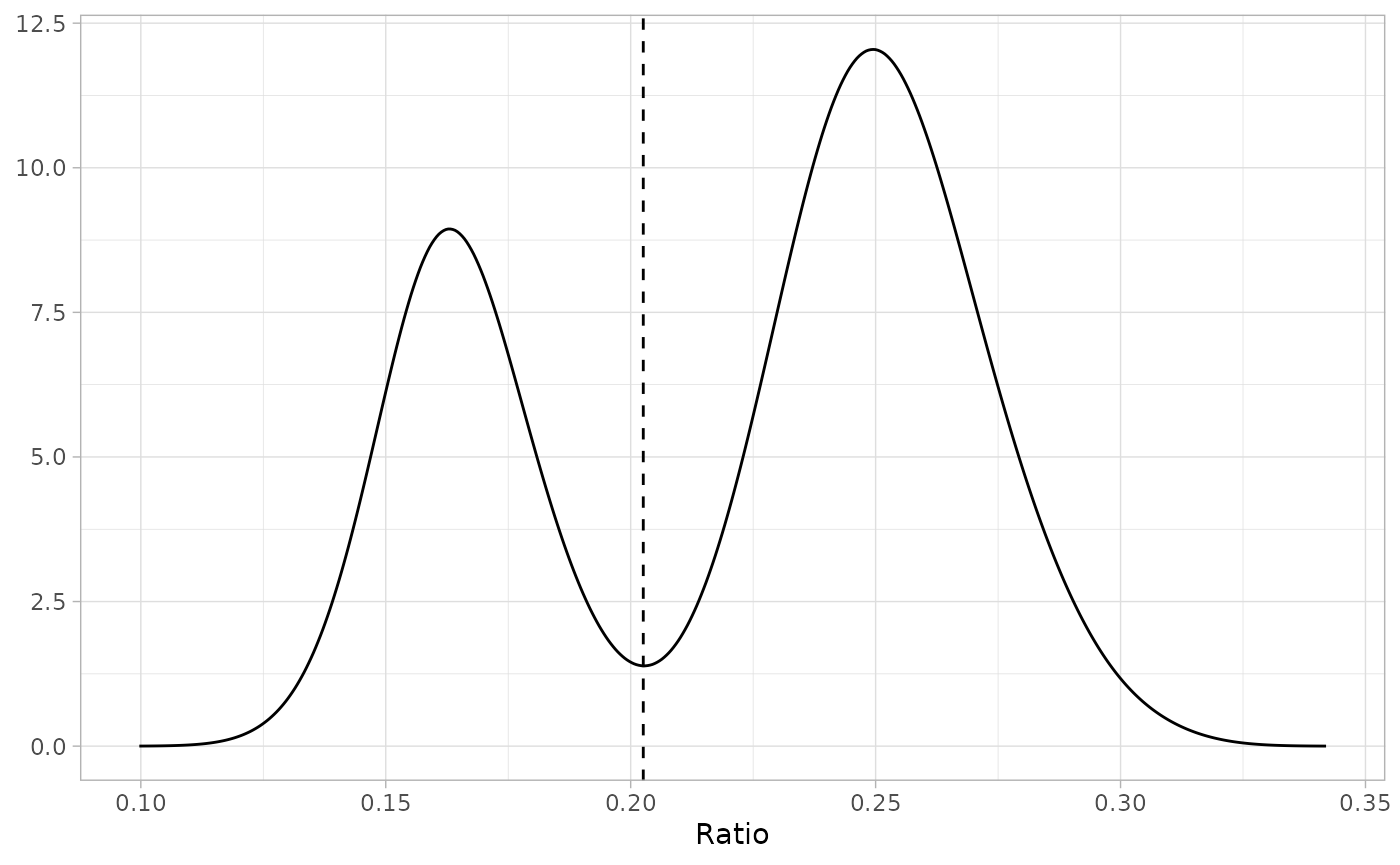
ggplot() +
geom_point(data = fc, aes(x, y), alpha = 0.4) +
labs(x = "CW (mm)", y = "CH (mm)", ) +
mytheme + geom_abline(slope = disc, color = "red", linewidth = 1.3)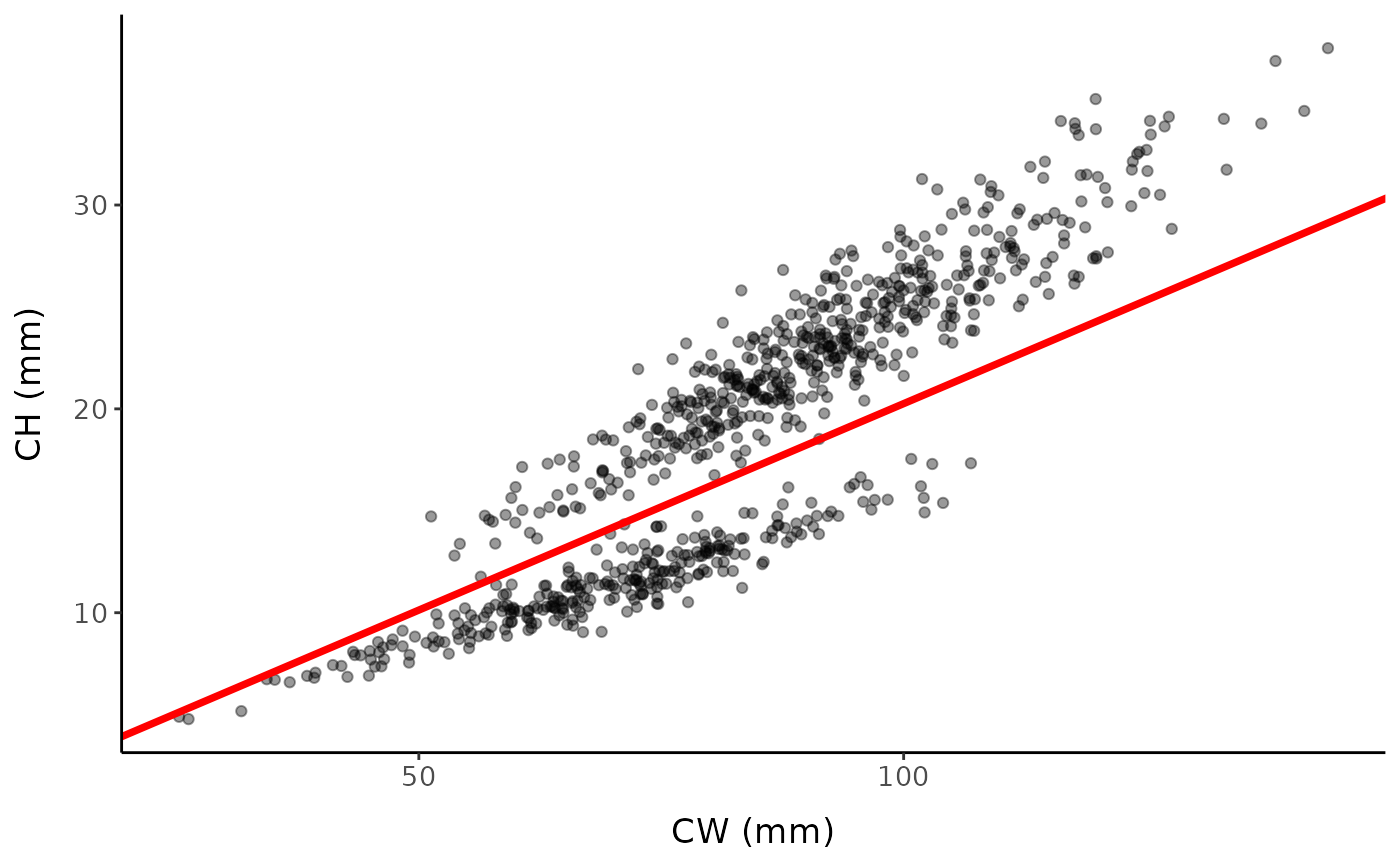
Simulated data with addition of linear discriminant function identified via the inflection point method
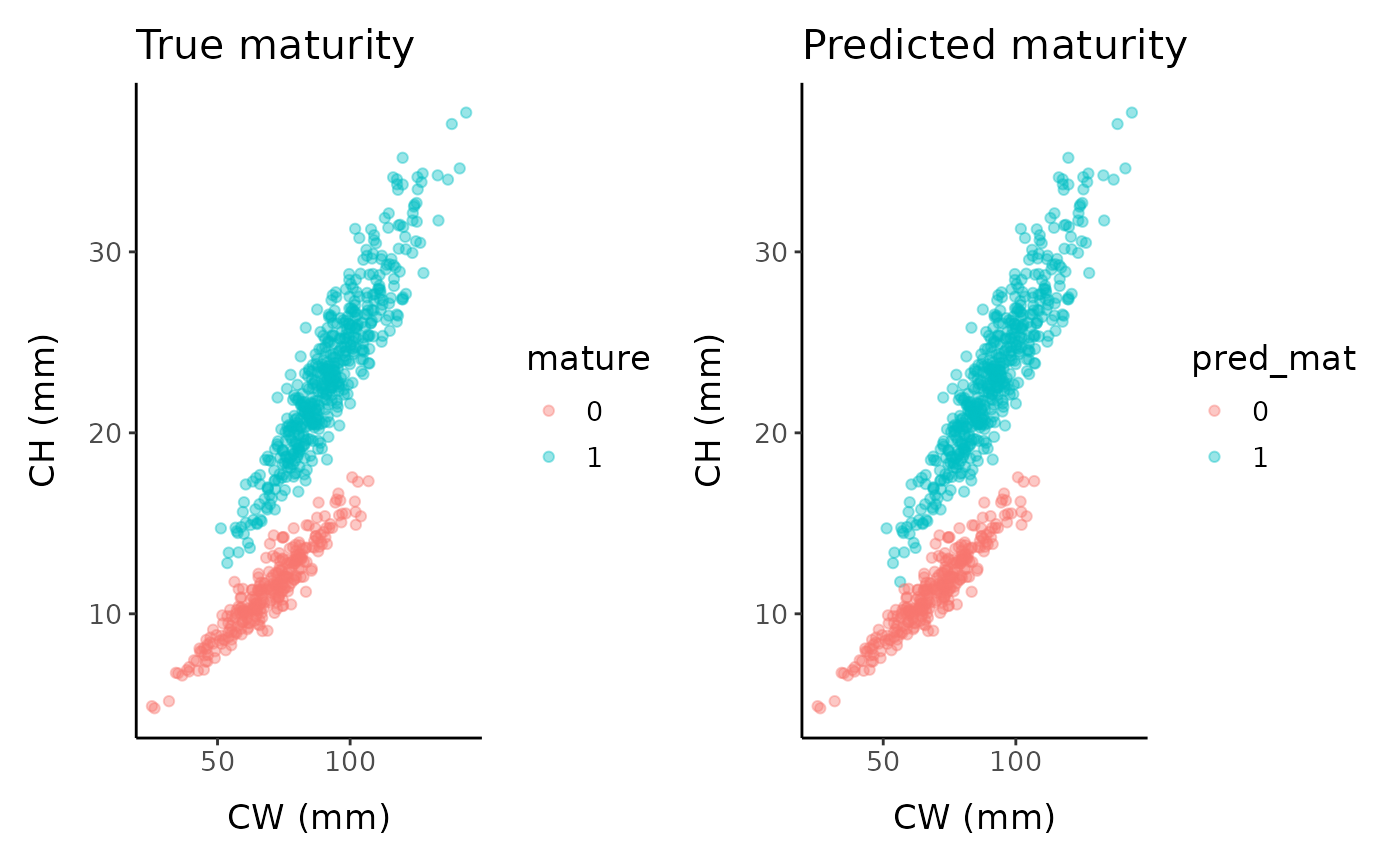
The line can then be used to classify each point as immature and mature, enabling logistic regression to be applied to estimate SM50:
fc_infl_pt <- fc %>% mutate(pred_mat = as.factor(if_else(y / x > disc, 1, 0)),
correct = if_else(pred_mat == mature, TRUE, FALSE))
if (rlang::is_installed("patchwork")) {
(ggplot() +
geom_point(data = fc_infl_pt, aes(x, y, color = mature), alpha = 0.4) +
labs(x = "CW (mm)", y = "CH (mm)", title = "True maturity") +
mytheme) +
(ggplot() +
geom_point(data = fc_infl_pt, aes(x, y, color = pred_mat), alpha = 0.4) +
labs(x = "CW (mm)", y = "CH (mm)", title = "Predicted maturity") +
mytheme)
} else {
ggplot() +
geom_point(data = fc_infl_pt, aes(x, y, color = mature), alpha = 0.4) +
labs(x = "CW (mm)", y = "CH (mm)", title = "True maturity") +
mytheme
ggplot() +
geom_point(data = fc_infl_pt, aes(x, y, color = pred_mat), alpha = 0.4) +
labs(x = "CW (mm)", y = "CH (mm)", title = "Predicted maturity") +
mytheme
}
Comparing methods
all_clusters <- cluster_mods(fc, xvar = "x", yvar = "y", method = c("all"), plot = TRUE)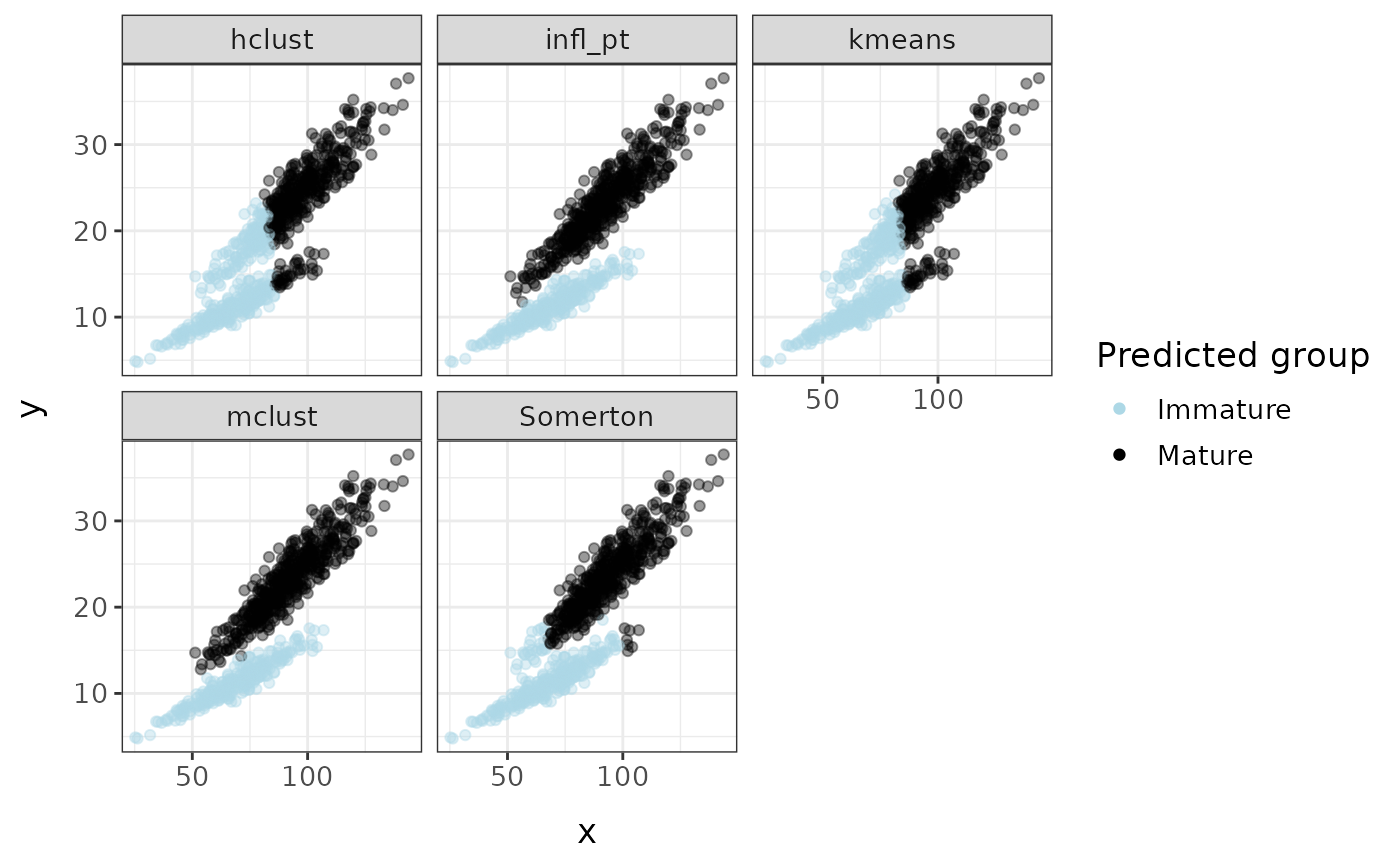
Post-classification logistic regression
Once a method of maturity classification has been identified, many additional choices need to be made when using logistic regression to obtain an estimate of SM50, particularly if you want to obtain standard errors, confidence intervals, etc. This aspect of the analysis is the same as determining size at maturity for non-crustacean fisheries.
The most common way to do this is to fit a generalized linear model using the binomial family with a logit link, then taking the ratio of the estimated coefficients to find the SM50 value. For example, using the classifications produced by the Somerton method:
infl_pt_mod <- glm(pred_mat ~ x,
family = binomial(link = "logit"),
data = fc_infl_pt)
# SM50 = -A/B
unname(-coef(infl_pt_mod)[1] / coef(infl_pt_mod)[2])
#> [1] 74.85785See the article on post-classification logistic regression for more details on options for methods to obtain SM50 values and confidence intervals once your data set includes maturity labels.
